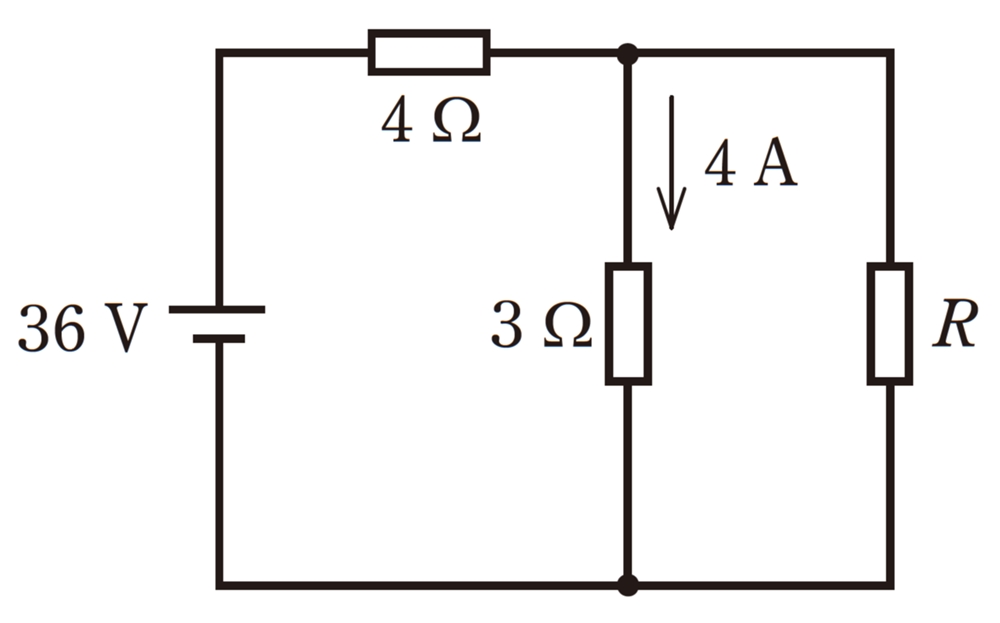
図のような直流回路において,抵抗3Ωには4Aの電流が流れている。抵抗Rにおける消費電力[W]は。
答え
イ.6
ロ.12
ハ.24
ニ.36
『出典:令和5年度第一種電気工事士筆記試験【午前】(問2)』
解説
正解は「ハ.24」です。
この問題のポイントは、オームの法則のについてです。
一見すると難しいと感じますが、オームの法則を使い一つずつ値を導いていきましょう。
求めた値を図に書き込みながら解いていきましょう。

ボルベア
一つずつ解いていこう!
解き方
抵抗3Ωにかかる電圧V3を求める
抵抗3ΩをR3とします。そして4Aの電流が流れているので、R3にかかる電圧V3を求めます。
\(V_3=IR_3\\~~~~=4\times3\\~~~~=12[V]\)
抵抗4Ωにかかる電圧V4を求める
抵抗4ΩをR4とします。R4とR3は直列に接続されているので、R4にかかる電圧V4は電源電圧VからV3を引いた値となります。
\(V_4=V-V_3\\~~~~=36-12\\~~~~=24[V]\)
回路全体に流れる電流Iを求める
R4とV4から回路全体に流れる電流Iが求められます。
\(I=\Large{\frac{V_4}{R_4}}\\~~=\Large{\frac{24}{4}}\\~~=6[A]\)
抵抗Rに流れる電流IRを求める
抵抗Rに流れる電流IRを求めます。電流IがR3とRに分流するので、次の式で求められます。
\(I_R=I-I_3\\~~~~=6-4\\~~~~=2[A]\)
抵抗Rを求める
抵抗Rはこれまでに求めた電流IRと電圧V3から求められます。
\(R=\Large{\frac{V_3}{I_R}}\\~~~=\Large{\frac{12}{2}}\\~~~=6[Ω]\)
抵抗Rの消費電力Pを求める
消費電力Pは次の式で求められます。
\(P={I_R}^{2}R\\~~~=2^{2}\times6\\~~~=24[W]\)






















コメント