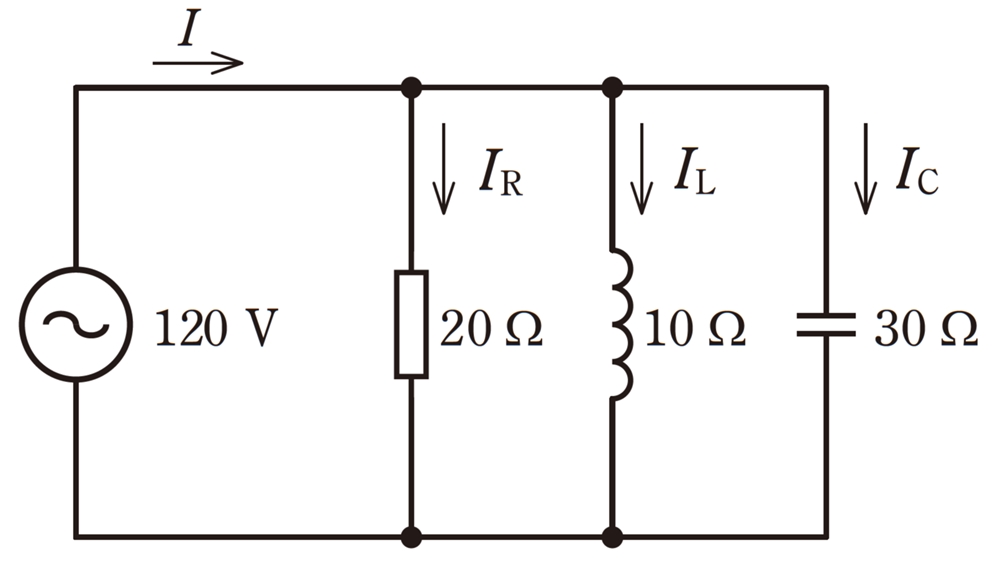
図のような交流回路において，電源電圧120V，抵抗20Ω，誘導性リアクタンス10Ω，容量性リアクタンス30Ωである。図に示す回路の電流I［A］は。
答え
イ．8
ロ．10
ハ．12
ニ．14
『出典：令和5年度第一種電気工事士筆記試験【午後】（問3）』
解説
正解は「ロ．10」です。
この問題のポイントは、交流回路におけるリアクタンスの扱いについてです。
問題の回路では誘導性リアクタンスと容量性リアクタンスがあります。これらは単位はΩですが、単純に抵抗として扱うことはできません。
今回はそれぞれに流れる電流を求めてから合成して、回路全体の電流を求めます。
ボルベア
リアクタンスに流れる電流は単純に足し算できない！
解き方
抵抗に流れる電流IRを求める
抵抗に流れる電流IRを求めます。
\(I_R=\Large{\frac{V}{R}}\\~~~~=\Large{\frac{120}{20}}\\~~~~=6［A］\)
コイルに流れる電流ILを求める
抵抗に流れる電流IRを求めます。
\(I_R=\Large{\frac{V}{R}}\\~~~~=\Large{\frac{120}{20}}\\~~~~=6［A］\)
コンデンサに流れる電流ICを求める
抵抗に流れる電流IRを求めます。
\(I_R=\Large{\frac{V}{R}}\\~~~~=\Large{\frac{120}{30}}\\~~~~=4［A］\)
電流ILと電流ICを合成する
電流ILと電流ICは逆向きに流れます。よって打ち消し合うので、差し引きで合成できます。
今回は絶対値が必要なので、大きい方から小さい方を引きます。
\(I_{LC}=I_L-I_C\\~~~~~=12-4\\~~~~~=8［A］\)
電流を合成して電流Iを求める
電流の合成は、インピーダンスZと同じような式で求める事ができます。
\(I=\sqrt{{I_R}^2+{I_{LC}}^2}\\~~~=\sqrt{6^2+8^2}\\~~~=\sqrt{36+64}\\~~~=\sqrt{100}\\~~~=10［A］\)
コメント