電気工事士試験では、頻繁にインピーダンス(Z)を求める問題が出題されます。
インピーダンスを求める問題もあれば、他のものを求める途中で計算が必要な場合もあります。
インピーダンスは必ず覚えておきたい必須項目です。
インピーダンスの基礎
インピーダンスとは交流回路における抵抗を表します。記号はZを用い、単位は[Ω]です。
抵抗と言えばRを思い浮かべますが、交流回路ではRだけが抵抗でありません。
インピーダンス(Z)は抵抗(R)とリアクタンス(X)から成り立ちます。またリアクタンス(X)は、誘導性リアクタンス(XL)と容量性リアクタンス(XC)に分けられます。
それぞれには位相があり、関係性は次の図の通りです。
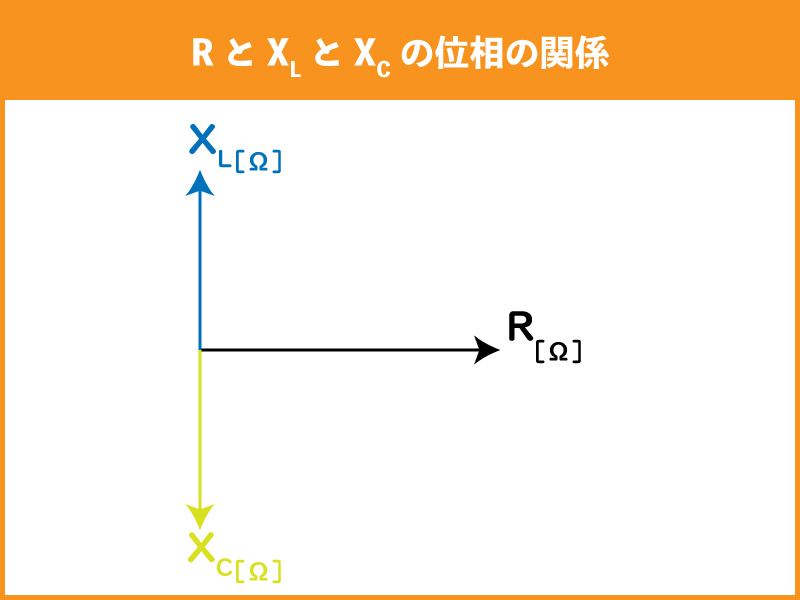
図から分かるように、XLとXCは逆向きの関係性があります。これはお互いの大きさを単純に差し引きできます。
しかし抵抗(R)とリアクタンス(X)は位相が90°違うので、単純に足し算はできません。
インピーダンスの公式
インピーダンス(Z)は、抵抗(R)とリアクタンス(X)から、次の式で求められます。
\(Z=\sqrt{R^{2}+X^{2}}[Ω]\\~~~=\sqrt{R^{2}+(X_L-X_C)^{2}}~~~~or~~~~\sqrt{R^{2}+(X_C-X_L)^{2}}[Ω]\)
リアクタンス(X)は前述の通り、互いに打ち消しあいます。
ポイントは、必ず大きい方から小さい方を減算しましょう。値が必ず正数とならなければいけません。負数となって抵抗から減算しないようにしましょう。
また誘導性リアクタンス(XL)と容量性リアクタンス(XC)がいずれかしかない場合は、減算せずにそのままの値をリアクタンス(X)として計算します。
練習問題
インピーダンス(Z)の公式を解説しました。
ここからは公式を使って、練習問題を解いていきます。
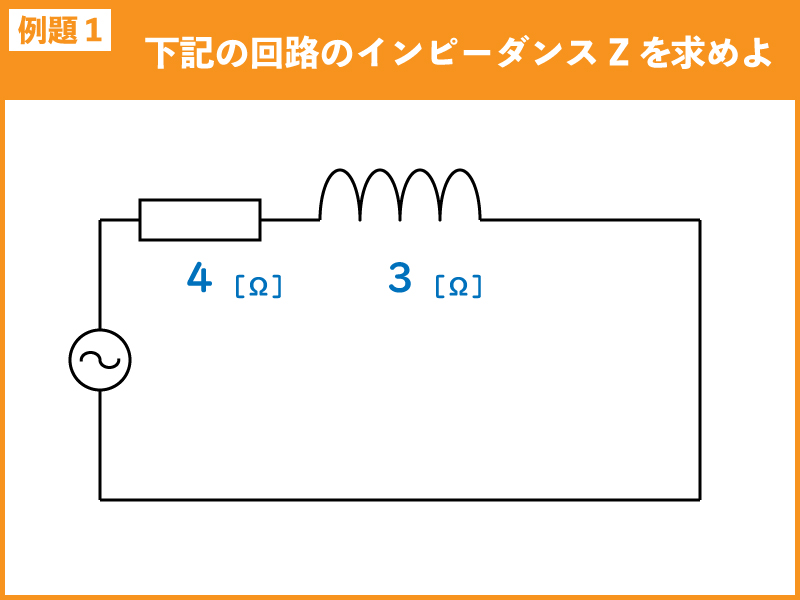
例題1
下記の回路のインピーダンス[Ω]を求めよ。
解説
例題1の回路では、抵抗Rと誘導性リアクタンス(XL)の直列回路なので、下記の式で求められます。
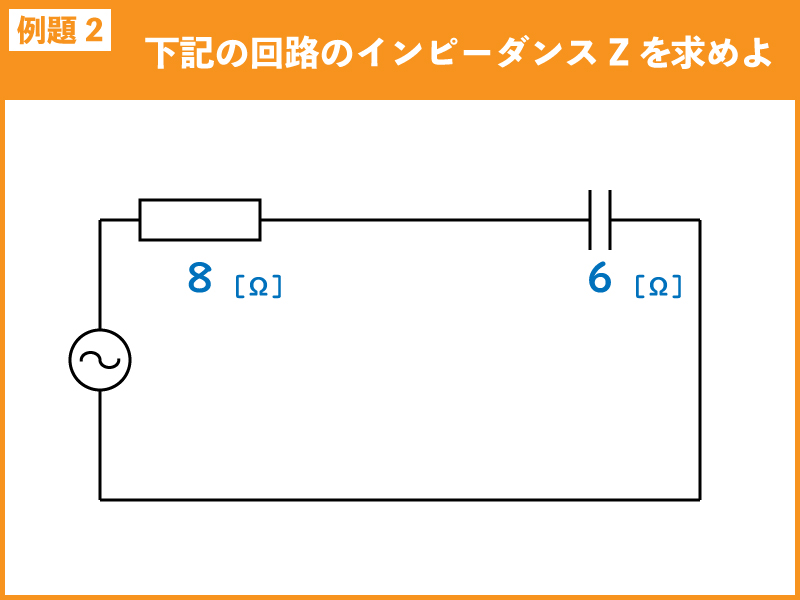
例題2
下記の回路のインピーダンス[Ω]を求めよ。
解説
例題2の回路では、抵抗Rと容量性リアクタンス(XC)の直列回路なので、下記の式で求められます。
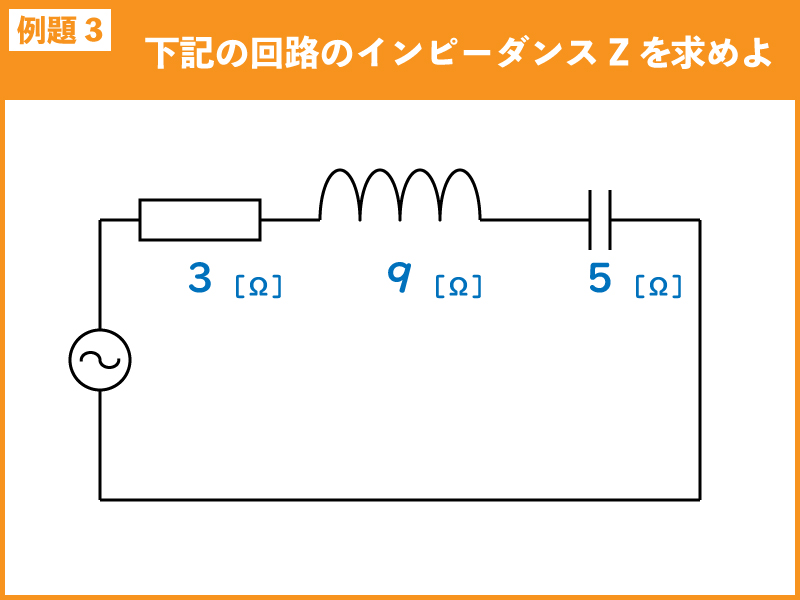
例題3
下記の回路のインピーダンス[Ω]を求めよ。
解説
例題3の回路では、抵抗Rと誘導性リアクタンス(XL)と容量性リアクタンス(XC)の直列回路です。
誘導性リアクタンス(XL)と容量性リアクタンス(XC)を比較するとXLが大きいので、XLからXCを減算します。
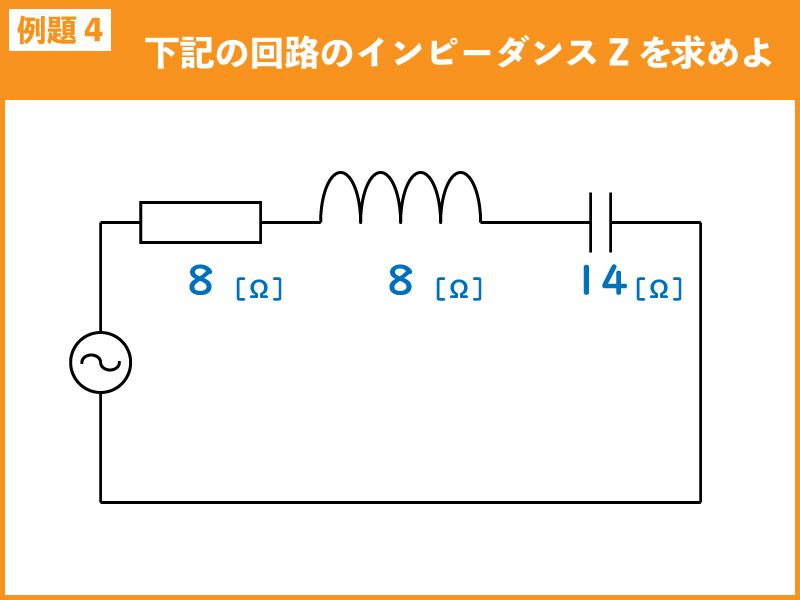
例題4
下記の回路のインピーダンス[Ω]を求めよ。
解説
例題4の回路では、抵抗Rと誘導性リアクタンス(XL)と容量性リアクタンス(XC)の直列回路です。
誘導性リアクタンス(XL)と容量性リアクタンス(XC)を比較するとXCが大きいので、XCからXLを減算します。






















コメント