電線の抵抗値を求める公式

電気工事士試験の筆記試験では、電線の抵抗値に関する問題が出題されます。

また計算問題以外にも電線の抵抗値に関する問題が出題されるので、考え方を理解しておきましょう。

電線の抵抗値の考え方

電線は電気を通すための導体ですが、僅かながら抵抗があります。

負荷の抵抗に比べるとかなり小さいものなので、基本的には無視して計算しています。しかし配電線などの長距離になると無視できない値となるので、電線の抵抗値も重要となってきます。

これらのことから電気工事士試験では、電線の抵抗値に関する問題が出題されます。

また電線の抵抗値を電気抵抗R［Ω］と表します。

電気抵抗Rを決める要素

電気抵抗R［Ω］を決める要素には、次のものがあります。

これらは理屈よりもイメージで覚えておいた方が良いです。計算問題だけでなく、知識問題でも必要となる場面があるので、しっかりと覚えておきましょう。

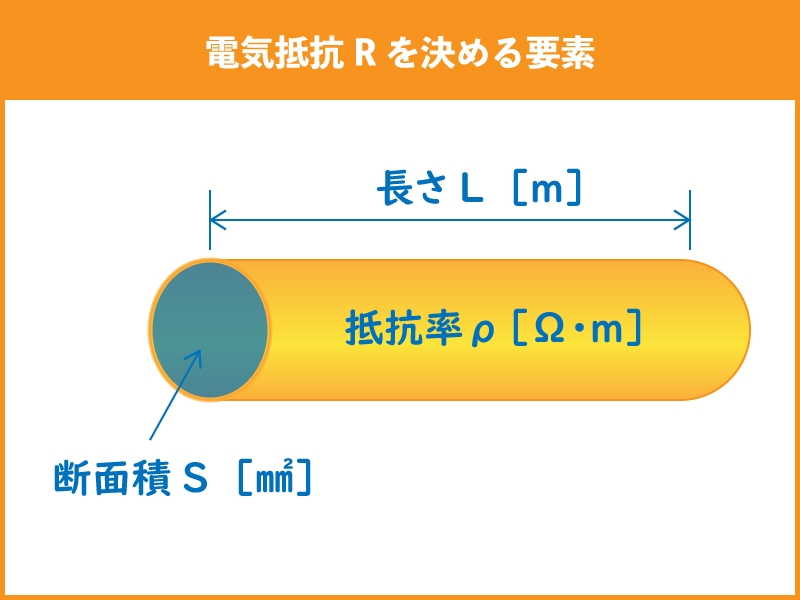
長さL［ⅿ］

長さLは、電線の距離です。単位は［ⅿ］となります。

抵抗値は、電線が長くなるにつれて大きくなります。

長くなるほど、抵抗が直列に接続されていくイメージですね。

同じ太さの電線で比較すると、長さが2倍になれば抵抗値は2倍となります。

よって電気抵抗Rは、長さLに比例します。

断面積S［㎡］

断面積Sは、電線の太さです。単位は［㎡］となります。

試験問題では単位が［㎟］となっている場合があるので、換算しないといけないので注意しましょう。

抵抗値は、電線の太さが大きくなるにつれて低くなります。

同じ長さの電線で比較すると、太さが2倍になれば抵抗値は1/2倍となります。

よって電気抵抗Rは、断面積Sに反比例します。

抵抗率ρ［Ω･ⅿ］

抵抗率ρは、電線の電気の通しやすさです。単位は［Ω･ⅿ］となります。また「ρ」はギリシャ文字で「ロー」と読みます。

抵抗率ρは、導体の種類ごとに決まっている固有の値です。係数と考えましょう。

抵抗率ρが小さいほど、電気抵抗Rは小さくなります。

同じ長さ、太さの電線で比較すると、導体の種類が違えば抵抗値も変わってきます。

電線の抵抗値の公式

ここからは電線の電気抵抗Rを求める公式について解説します。

電気抵抗Rを求める公式は、太さの単位によって2種類に分かれます。

基本的には同じ式ですが、直径［ｍ］の場合は断面積［㎡］に変換する必要があります。

電線の太さが断面積［㎡］の場合

電線の太さが断面積S［㎡］の場合は、次の式で電気抵抗Rが求められます。

前述のとおり、長さに比例して太さに反比例しています。

電線の太さが直径［ｍ］の場合

電線の太さが直径D［ｍ］の場合は、次の式で電気抵抗Rが求められます。

複雑に見えますが、直径Dを断面積Sに変換しているだけです。

断面積Sは半径×半径×πなので、直径Dで表すと次の式になります。

この式を断面積［㎡］の場合の式に代入すると、直径［ⅿ］の場合の式となりますね。

練習問題

電気抵抗の公式を解説しました。

ここからは公式を使って、実際に出題される練習問題を解いていきます。

例題1

電気抵抗R［Ω］、断面積S［㎟］、長さL［ⅿ］の導体の抵抗率ρ［Ω･ⅿ］を表す式は。

解説

抵抗率ρ［Ω･ⅿ］を表す式は、公式を変形すれば導けます。

また断面積の単位が［㎟］なので、［㎡］へ変換しましょう。［㎟］を［㎡］にするには10^-6を乗算します。

例題2

電気抵抗R［Ω］、直径D［㎜］、長さL［ⅿ］の導体の抵抗率ρ［Ω･ⅿ］を表す式は。

解説

抵抗率ρ［Ω･ⅿ］を表す式は、公式を変形すれば導けます。

また直径の単位が［㎜］なので、［ⅿ］へ変換しましょう。㎜］を［ⅿ］にするには10^-3を乗算します。