電気工事士の筆記試験において、たまに出題される問題があります。
「直流回路において、コイル及びコンデンサに蓄えられるエネルギーを求めよ。」
ぱっと見は難しそうに思える問題です。また直流回路なのが、厄介に感じます。
しかしこの問題は、簡単な公式を覚えておくだけで解くことができます。

公式は簡単だから、覚えておこう!
コイルに蓄えられるエネルギーの公式
下記のような直流回路において、コイル(L)に蓄えられるエネルギーはどの様に求められるでしょうか。
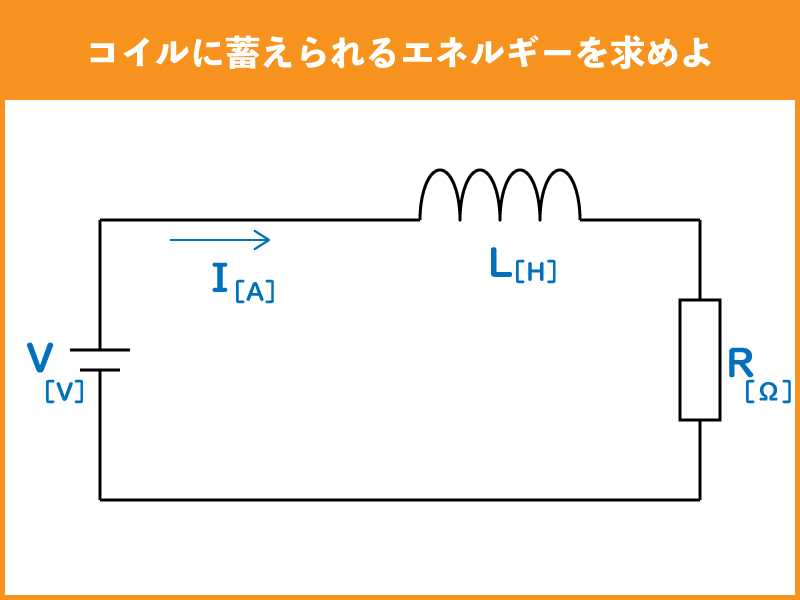
コイル(L)に蓄えられるエネルギーを磁気エネルギーとも呼び、ここではWLとします。
磁気エネルギー(WL)は次の式から求められます。
\(W_L=\Large{\frac{1}{2}}\normalsize{LI^{2}}[J]\)
磁気エネルギー(WL)の単位は[J(ジュール)]です。
この様に磁気エネルギーは、コイルの自己インダクタンス(L)とコイルに流れる電流(I)から求めらます。

磁気エネルギーは、コイルに流れる電流がポイント!
コンデンサーに蓄えられるエネルギーの公式
下記のような直流回路において、コンデンサ(C)に蓄えられるエネルギーはどの様に求められるでしょうか。
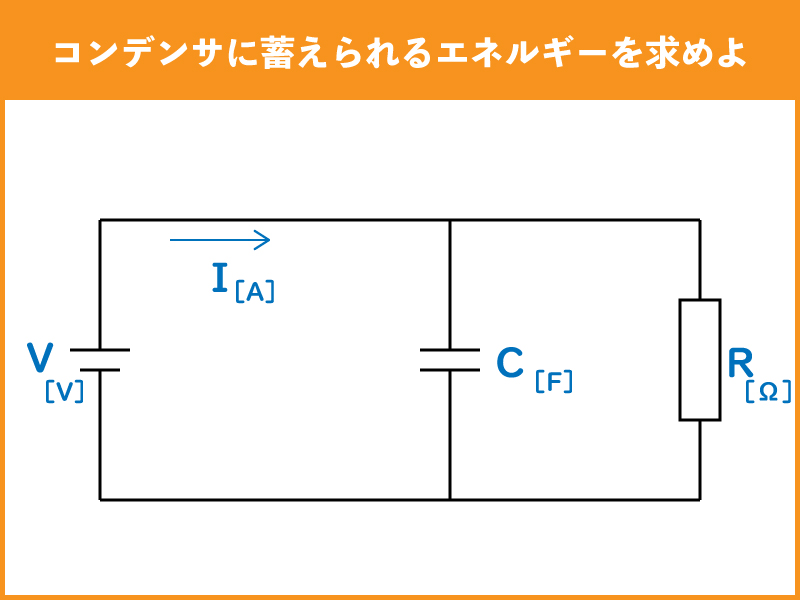
コンデンサ(C)に蓄えられるエネルギーを静電エネルギーとも呼び、ここではWCとします。
静電エネルギー(WC)は次の式から求められます。
\(W_C=\Large{\frac{1}{2}}\normalsize{CV^{2}}[J]\)
静電エネルギー(WC)の単位は[J(ジュール)]です。
この様に静電エネルギーは、コンデンサの静電容量(C)とコンデンサにかかる電圧(V)から求めらます。

静電エネルギーは、コンデンサにかかる電圧がポイント!
練習問題
磁気エネルギー(WL)及び静電エネルギー(WC)の公式を解説しました。
ここからは公式を使って、練習問題を解いていきます。
例題1
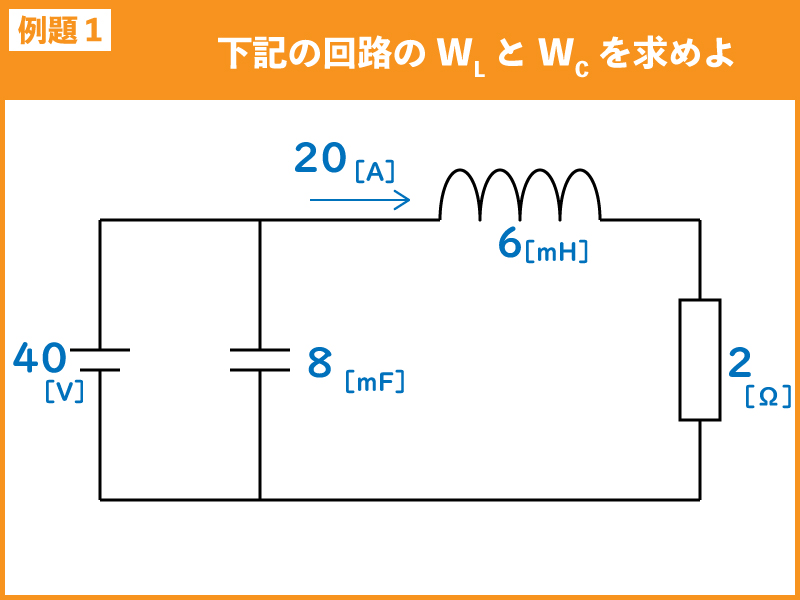
下記の直流回路において、コイル(L)及びコンデンサ(C)それぞれに蓄えられるエネルギーWLとWCを求めよ。
解説
まずはWLを求めます。WLを求めるにはL[H]とコイルに流れる電流が必要です。
どちらも図に提示してあるので、それらを公式に当てはめて求めます。
よって磁気エネルギーWLは1.2[J]となります。
次にWCを求めます。WCを求めるにはC[F]とコンデンサにかかる電圧が必要です。
図からC[F]の値と、コンデンサにかかる電圧が40Vだと分かります。これらを公式に当てはめて求めます。
よって静電エネルギーWCは6.4[J]となります。
例題2
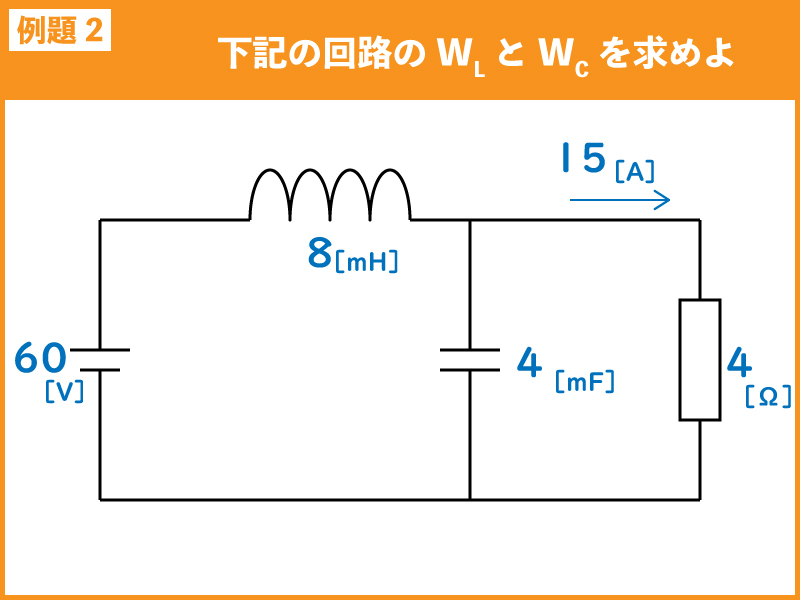
下記の直流回路において、コイル(L)及びコンデンサ(C)それぞれに蓄えられるエネルギーWLとWCを求めよ。
解説
まずはWLを求めます。WLを求めるにはL[H]とコイルに流れる電流が必要です。
コイルに流れる電流は、抵抗に流れる電流と同じで15[A]となります。
これは直流回路において、コンデンサは開放と見なせるので、コイルと抵抗の直列回路となります。コンデンサで分流はされません。
これらを公式に当てはめて求めます。
よって磁気エネルギーWLは0.9[J]となります。
次にWCを求めます。WCを求めるにはC[F]とコンデンサにかかる電圧が必要です。
コンデンサにかかる電圧は、抵抗にかかる電圧と同じで60[V]となります。
これは直流回路において、コイルは短絡と見なせるので、コンデンサと抵抗の並列回路となります。コイルで分圧はされません。
これらを公式に当てはめて求めます。
よって静電エネルギーWCは7.2[J]となります。






















コメント