【令和2年度】第一種電気工事士《筆記試験》問5

問題

図のような三相交流回路において， 電源電圧は200V, 抵抗は20Ω, リアクタンスは40Ωである。この回路の全消費電力[kW]は。

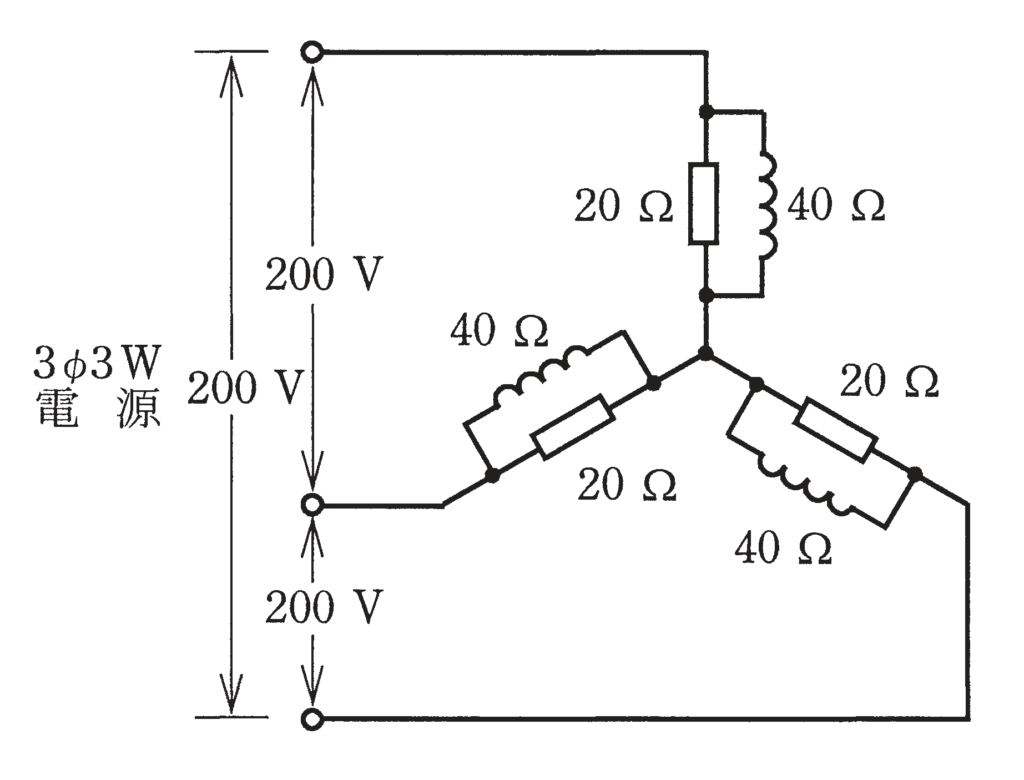
答え

イ．1.0

ロ．1.5

ハ．2.0

ニ．12

『出典：令和2年度第一種電気工事士筆記試験(問5)』

解説

正解は「ハ．2.0」です。

この問題のポイントは、求められているのが消費電力ということです。消費電力は抵抗分でしか発生しません。なので抵抗に流れる電流を求めれば、自ずと消費電力が求められます。

解き方

抵抗に流れる電流を求める

抵抗に流れる電流を求めます。

電圧は線間電圧が200Vなので、相電圧に変換する必要があります。次の式で求められます。

\(相電圧=\Large{\frac{線間電圧}{\sqrt{3}}}\\~~~~~~~~~~=\Large{\frac{200}{\sqrt{3}}}\)

これを使って、抵抗に流れる電流を求めます。オームの法則より、次の式で求められます。

\(I_R＝\Large{\frac{V}{R}}\\~~~~＝\Large{\frac{\Large{\frac{200}{\sqrt{3}}}}{20}}\\~~~~＝\Large{\frac{200}{20\sqrt{3}}}\\~~~~＝\Large{\frac{10}{\sqrt{3}}}\)

全消費電力を求める

三相交流回路の全消費電力は、次の式で求められます。

\(P=\sqrt{3}VI_R\\~~~~＝\sqrt{3}\times200\times\Large{\frac{10}{\sqrt{3}}}\\~~~~＝2000[W]\\~~~~＝2[kW]\)

ちなみにこの式は、抵抗とリアクタンスが並列接続してある回路のみで有効です。直列接続の場合は、次の式になります。

\(P=\sqrt{3}VI\cos\theta\)