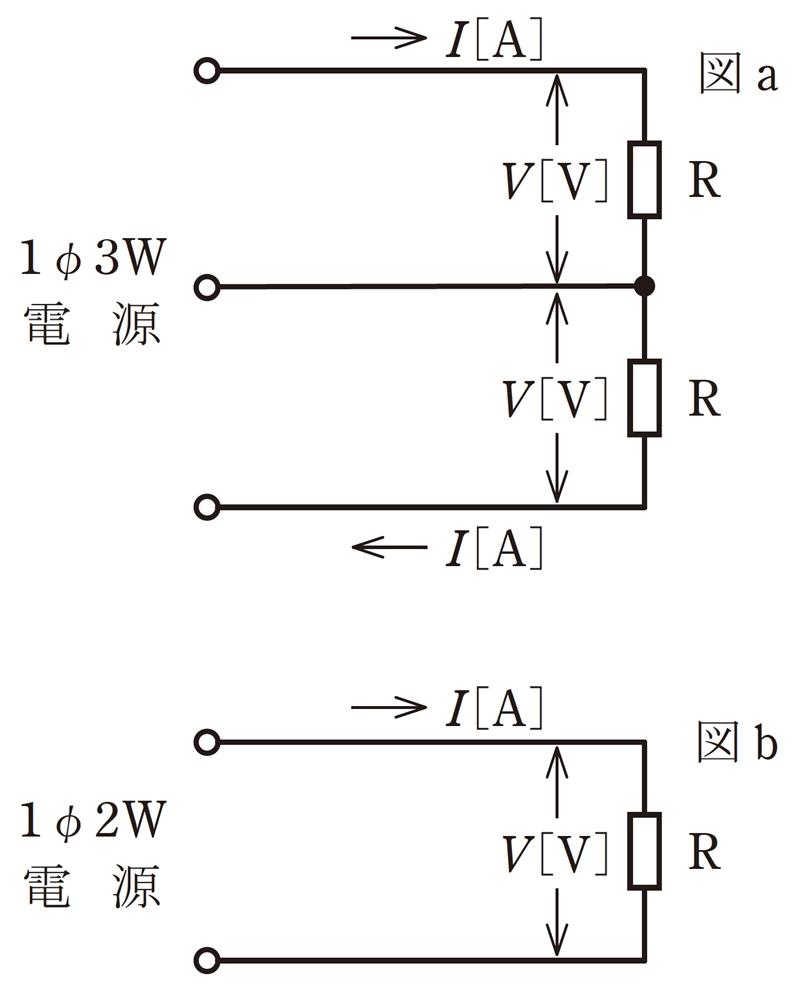
図aのような単相3線式電路と,図bのような単相2線式電路がある。図aの電線1線当たりの供給電力は,図bの電線1線当たりの供給電力の何倍か。
ただし,Rは定格電圧V[V]の抵抗負荷であるとする。
答え
イ.\(\Large{\frac{1}{3}}\)
ロ.\(\Large{\frac{1}{2}}\)
ハ.\(\Large{\frac{4}{3}}\)
ニ.\(\Large{\frac{5}{3}}\)
『出典:令和5年度第一種電気工事士筆記試験【午後】(問6)』
解説
正解は「ハ.\(\Large{\frac{4}{3}}\)」です。
この問題のポイントは、電路から供給される電力と電線1線当たりから供給される電力の関係です。
ぱっと見は理解しにくい問題ですが、考え方が分かれば簡単です。

ボルベア
電力の違いを考えよう!
解き方
図aの供給電力を考える
図aの全体的な供給電力を考えます。
単相回路では\(I^{2}R\)で電力が求められます。
これを問題の図aに当てはめて、全体的な供給電力(Pa0)は次のようになります。
\(P_{a0}=I^{2}\times2R\\~~~~~~=2I^{2}R\)
単相3線式では電線が3線あるので、1線当たりの供給電力は1/3となります。
よって図aの1線当たりの供給電力(Pa1)は、次のようになります。
\(P_{a1}=\Large{\frac{P_{a0}}{3}}\\~~~~~~=\Large{\frac{2I^{2}R}{3}}\)
図bの供給電力を考える
図bの全体的な供給電力を考えます。
単相回路では\(I^{2}R\)で電力が求められます。
これを問題の図bに当てはめて、全体的な供給電力(Pb0)は次のようになります。
\(P_{b0}=I^{2}\times1R\\~~~~~~=I^{2}R\)
単相2線式では電線が2線あるので、1線当たりの供給電力は1/2となります。
よって図bの1線当たりの供給電力(Pb1)は、次のようになります。
\(P_{b1}=\Large{\frac{P_{b0}}{2}}\\~~~~~~=\Large{\frac{I^{2}R}{2}}\)
図aと図bを比較する
問題で求められているのは、図aは図bの何倍かです。
この倍数をXとすると、次の式になります。
\(P_{a1}=P_{b1}\times{X}\\~~X=\Large{\frac{P_{a1}}{P_{b1}}}\\~~~~~=\Large{\frac{2I^{2}R}{3}}\normalsize{\times}\Large{\frac{2}{I^{2}R}}\\~~~~~=\Large{\frac{4}{3}}\)






















コメント