問題
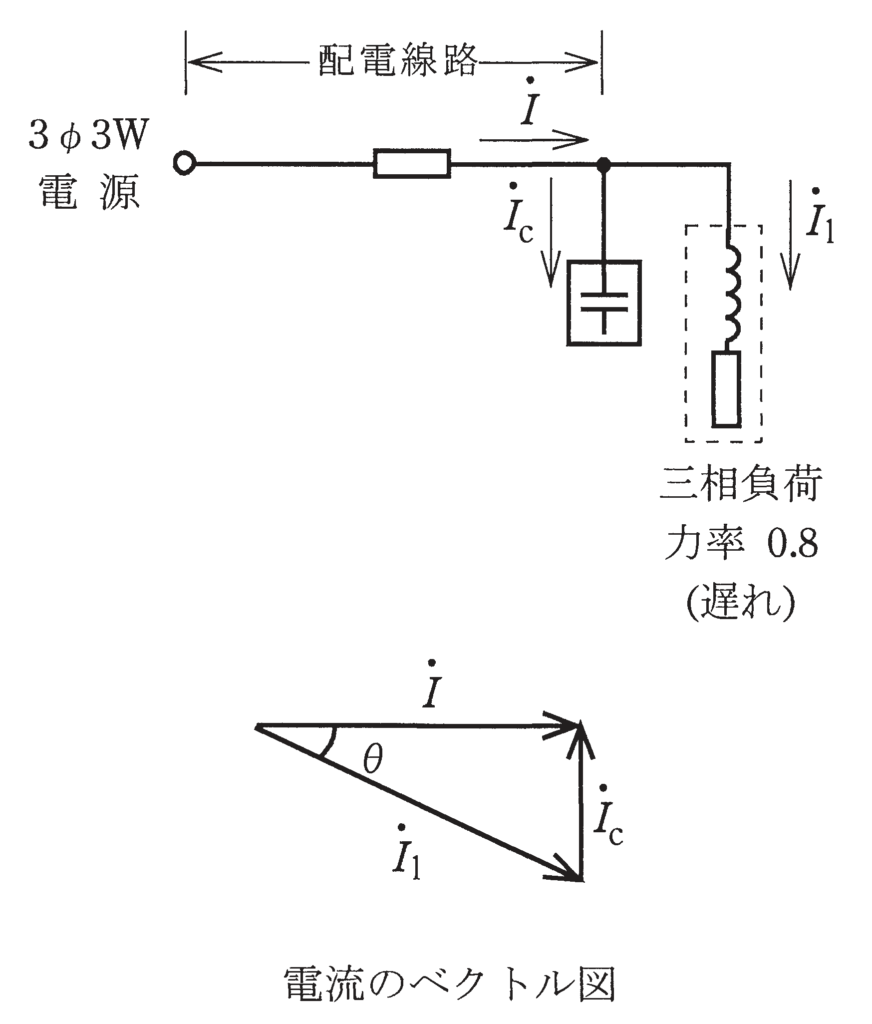
図のように,三相3線式構内配電線路の末端に,力率0.8(遅れ)の三相負荷がある。この負荷と並列に電力用コンデンサを設置して,線路の力率を1.0に改善した。コンデンサ設置前の線路損失が2.5kWであるとすれば,設置後の線路損失の値[kW]は。
ただし,三相負荷の負荷電圧は一定とする。
答え
イ.0
ロ.1.6
ハ.2.4
ニ.2.8
『出典:令和2年度第一種電気工事士筆記試験(問7)』
解説
正解は「ロ.1.6」です。
この問題のポイントは、線路損失と力率改善の関係についてです。
比較的に難しい問題です。
線路損失の公式に力率が関係するかを考えましょう。

ボルベア
線路損失の式を展開しよう!
解き方
線路損失と力率の関係
まず線路損失の式と力率の関係について考えます。線路損失PLは次の式で求められます。
\(P_L=3I^2R\)
また、電流Iは次の式になります。
\(I=\Large{\frac{P}{\sqrt{3}V\cos\theta}}\)
これを線路損失PLの式に代入して整理すると次のようになります。
\(P_L=3I^2R\\~~~~=3\left(\Large{{\frac{P}{\sqrt{3}V\cos\theta}}}\right)^2R\\~~~~=3\times\Large{{\frac{P^2}{3(V\cos\theta)^2}}}\normalsize{R}\\~~~~=\Large{{\frac{P^2R}{{V}^2{\cos\theta}^2}}}\)
電力Pや電圧V、線路抵抗Rは問題より一定となっているので、まとめてaとすると次のようになります。
\(P_L=\Large{\frac{a}{\cos\theta^2}}\)
これにより線路損失PLは、力率の2乗に反比例している事がわかります。
またaについて、式を変形すると次のようになります。そしてこの式に力率改善前の数値を代入して、aを求めます。
\(a=P_L\cos\theta^2\\~~~~=2.5\times0.8^2\\~~~~=1.6\)
力率改善後の線路損失を計算する
力率改善後の線路損失について計算します。
線路損失PLは先程と同じ式を使用します。そこに力率改善前の数値で求めたaを代入し、力率改善後の線路損失を求めます。
\(P_L=\Large{\frac{a}{\cos\theta^2}}\\~~~~=\Large{\frac{1.6}{1^2}}\\~~~~=1.6[kW]\)






















コメント