【令和2年度】第一種電気工事士《筆記試験》問1

問題

図のように，静電容量6μFのコンデンサ3個を接続して，直流電圧120Vを加えたとき，
図中の電圧V1の値［V］は。

答え

イ．10

ロ．30

ハ．50

ニ．80

『出典：令和2年度第一種電気工事士筆記試験(問1)』

解説

正解は「ニ．80」です。

解き方を2通り紹介します。

解き方①

直列に接続された各コンデンサに蓄えられる電荷Q[C]は全て同じになります。また電荷Qは次の式で求められます。

\(Q=CV\)

これを使って答えを求めます。

コンデンサを合成する

まず3個のコンデンサをそれぞれをCとし、合成します。コンデンサは抵抗と違い、並列なら足し算、直列なら和分の積で求められます。

並列で接続される2個のコンデンサを合成したものをC2とすると、次の式になります。

\(C_2=C+C\\~~~~=6+6\\~~~~=12[μF]\)

次に直列で接続されるコンデンサCとC2を合成したものをC0とすると、次の式になります。

\(C_0＝\Large{\frac{CC_2}{C+C_2}}\\~~~~＝\Large{\frac{6×12}{6+12}}\\~~~~＝\Large{\frac{72}{18}}\\~~~~＝4[μF]\)

電荷Q[C]を求める

この全体の合成したコンデンサC0と電圧から電荷Q[C]を求めます。

\(Q＝C_0V\\~~~~＝4\times120\\~~~~＝480[C]\)

電荷Q[C]からV1を求める

各コンデンサに蓄えられる電荷Q[C]は等しいので、このQ[C]からV1を求めます。

Q＝CVを変形してV＝Q/Cにします。これから求めると次の式になります。

\(V_1＝\Large{\frac{Q}{C}}\\~~~~＝\Large{\frac{480}{60}}\\~~~~＝80[V]\)

解き方②

直列に接続されるコンデンサの分圧の公式があります。

これを覚えておくと簡単に解くことができます。

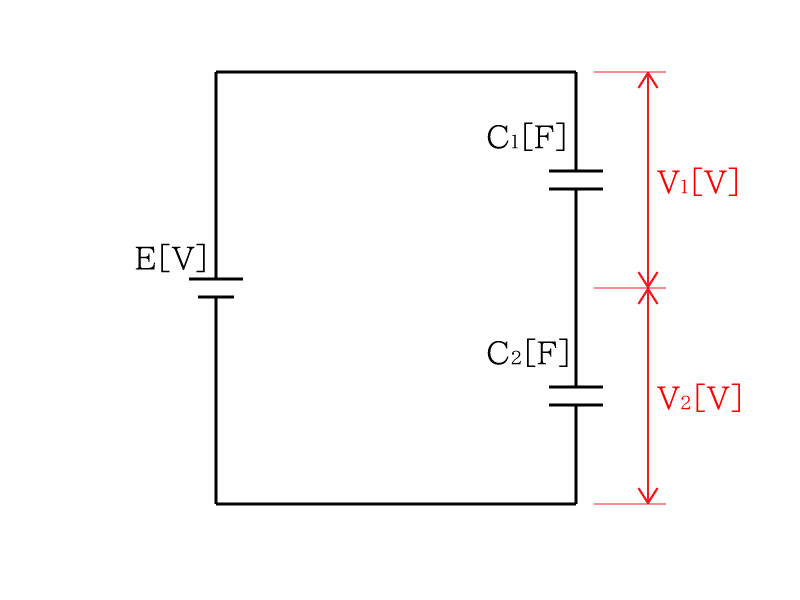
上記の図の場合に次の式が成り立ちます。

\(V_1＝\Large{\frac{ C_2 }{ C_1+C_2 }}\normalsize{E}\)

問題の図をこれに当てはめて求めると次のようになります。

コンデンサの並列部を合成する

まず並列で接続される2個のコンデンサを合成したものをC2とすると、次の式になります。

\(C_2=C+C\\~~~~=6+6\\~~~~=12[μF]\)

コンデンサの分圧の式から求める

コンデンサの分圧の式に当てはめて計算します。

\(V_1＝\Large{\frac{ C_2 }{ C_1+C_2 }}\normalsize{E}\\~~~~＝\Large{\frac{ 12 }{ 6+12 }}\normalsize{\times120}\\~~~~＝80[V]\)