【2019年度】第一種電気工事士《筆記試験》問9

問題

図のような直列リアクトルを設けた高圧進相コンデンサがある。電源電圧がV [V]，誘導性リアクタンスが9Ω，容量性リアクタンスが150Ω であるとき，この回路の無効電カ（設備容量）[var] を示す式は。

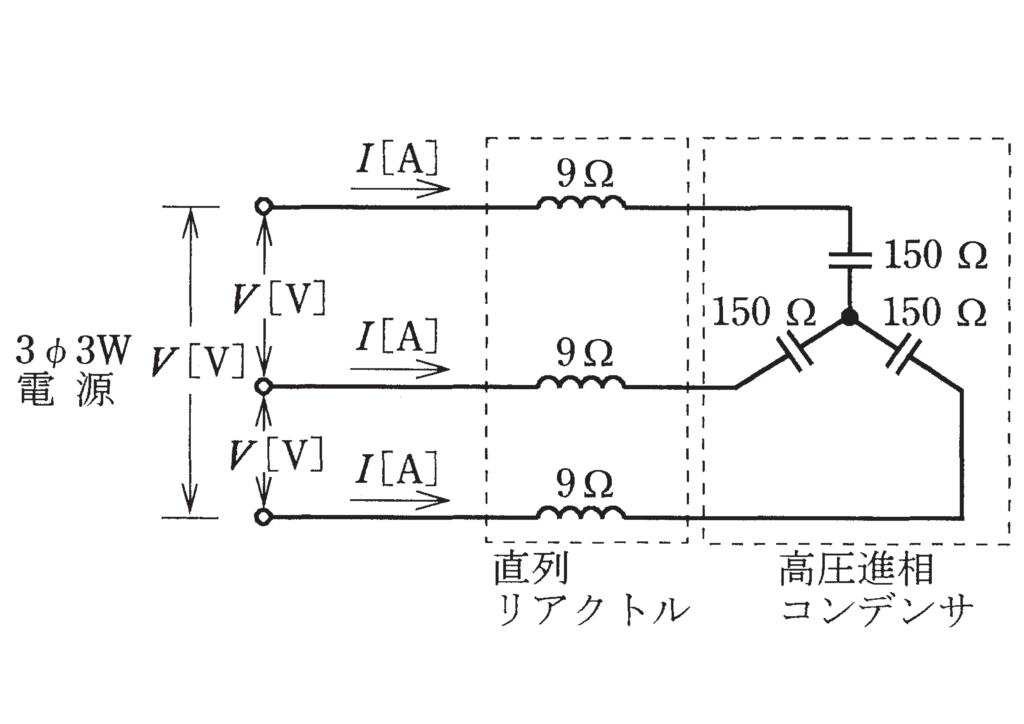
答え

イ．\(\Large{\frac{V^2}{159^2}}\)

ロ．\(\Large{\frac{V^2}{141^2}}\)

ハ．\(\Large{\frac{V^2}{159}}\)

ニ．\(\Large{\frac{V^2}{159}}\)

『出典：2019年度第一種電気工事士筆記試験(問9)』

解説

正解は「ニ．\(\Large{\frac{V^2}{159}}\)」です。

この問題のポイントは、リアクタンスの計算と無効電力の計算です。

リアクタンスを抵抗と考えて消費電力を計算するつもりですれば簡単です。

解き方

リアクタンスを合成する

この問題では、容量性リアクタンスと誘導性リアクタンスが直列に接続されています。容量性リアクタンスと誘導性リアクタンスは打ち消しあう性質があります。

こらから合成リアクタンスは差し引いたものになり、次の式の通りです。

\(X_C=150-9\\~~~~~~=141[Ω]\)

無効電力を求める

無効電力Q[var]は抵抗の時の消費電力の計算と同じで、抵抗が容量性リアクタンスに置き換わったと考えるといいです。

\(Q=I^2X_C=\Large{\frac{V^2}{X_C}}\)

今回は問題の選択肢に電圧しかないので、\(Q=\Large{\frac{V^2}{X_C}}\)を使います。

またY結線なので、電圧は相電圧である必要があります。相電圧は\(\Large{\frac{V}{\sqrt{3}}}\)になります。

また問題は三相回路なので全体は3倍する必要があります。これらをまとめて式にすると次の通りです。

\(Q＝3\Large{\frac{V^2}{X_C}}\\~~~~＝3\Large{\frac{{\Large({\frac{V}{\sqrt{3}}}})^2}{X_C}}\\~~~~＝3\Large{\frac{{\Large{\frac{V^2}{3}}}}{X_C}}\\~~~~＝3\times\Large{\frac{V^2}{3}}\normalsize{\times}\Large{\frac{1}{X_C}}\\~~~~＝\Large{\frac{V^2}{X_C}}\normalsize{[var]}\)

これに初めに計算したXCを代入すると次のようになります。

\(Q＝\Large{\frac{V^2}{X_C}}\\~~~~＝\Large{\frac{V^2}{141}}\normalsize{[var]}\)