問題
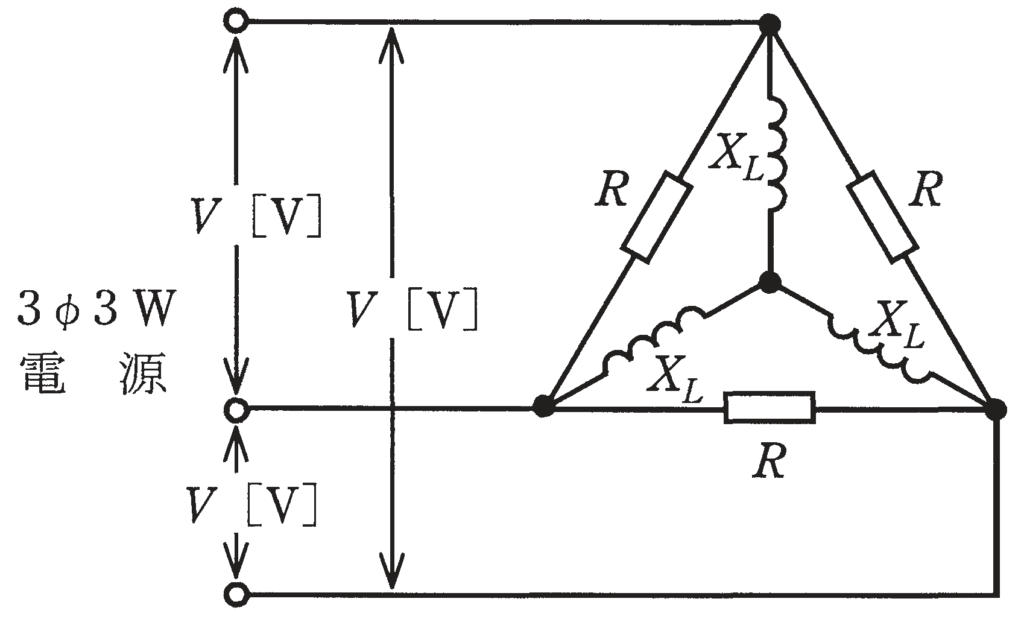
図のような三相交流回路において,電源電圧はV[V],抵抗R=5Ω, 誘導性リアクタンスXL=3Ωである。回路の全消費電力[W] を示す式は。
答え
イ.\(\Large{\frac{3V^2}{5}}\)
ロ.\(\Large{\frac{V^2}{3}}\)
ハ.\(\Large{\frac{V^2}{5}}\)
ニ.\(V^2\)
『出典:平成29年度第一種電気工事士筆記試験(問5)』
解説
正解は「イ.\(\Large{\frac{3V^2}{5}}\)」です。
この問題のポイントは、消費電力は抵抗でのみ発生ということです。
消費電力は抵抗分でしか発生しません。なので抵抗に流れる電流を求めれば、自ずと消費電力が求められます。
問題に誘導性リアクタンスがありますが、これは全く関係なく解くことができます。

ボルベア
消費電力は抵抗に流れる電流だけが関係する!
解き方
抵抗Rに流れる電流を求める
抵抗に流れる電流を求めます。
Δ結線なので、抵抗Rにかかる電圧はVです。
\(I_R=\Large{\frac{V}{R}}\)全消費電力を求める
消費電力は次の式で求められます。
\(P=I^2R\)しかし今回は三相交流回路で抵抗は3個あるので、先ほどの式を3倍する必要があります。
\(P=3I^2R\)この式に電流IRを代入します。
\(P=3{I_R}^2R\\~~~=3{I_R}^2R\\~~~=3{\Large({\frac{V}{R}})}^2R\\~~~=3{\Large{\frac{V^2}{R^2}}}R\\~~~={\Large{\frac{3V^2}{R}}}\)抵抗Rは5Ωなので答えは次のようになります。
\(P={\Large{\frac{3V^2}{5}}}\)





















コメント