問題
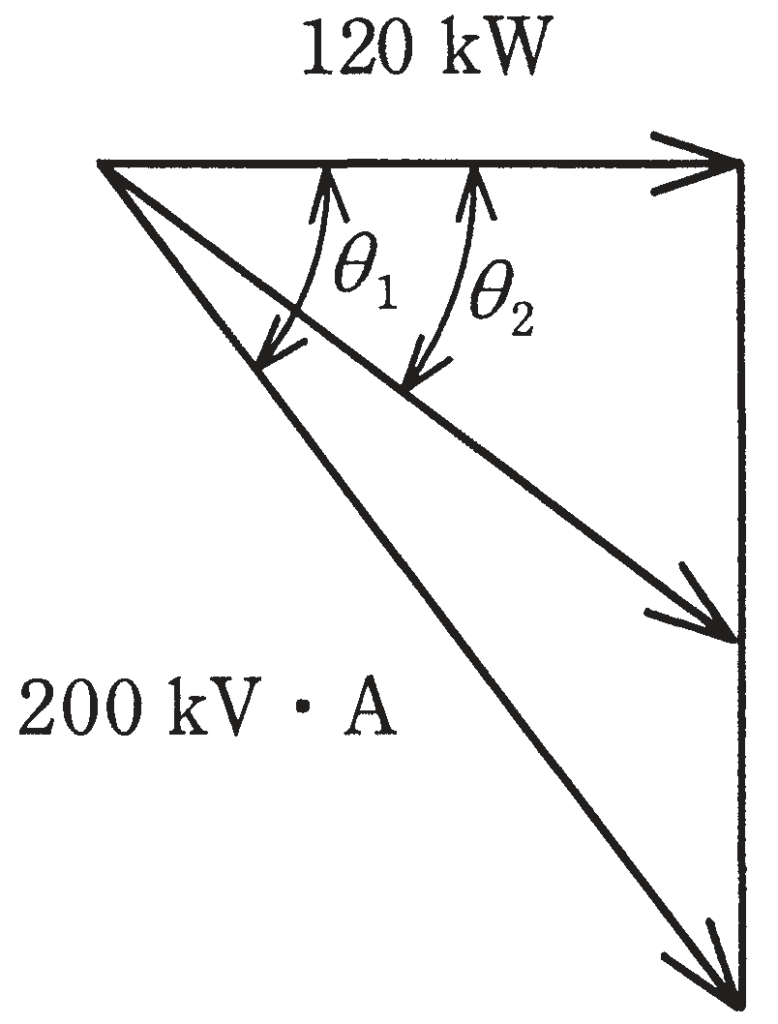
定格容量200kV・A, 消費電力120kW, 遅れ力率cosθ1=0.6の負荷に電力を供給する高圧受電設備に高圧進相コンデンサを施設して,力率をcosθ2=0.8に改善したい。必要なコンデンサの容量[kvar] は。
ただし,tanθ1=1.33, tanθ2=0.75とする。
答え
イ.35
ロ.70
ハ.90
ニ.160
『出典:平成29年度第一種電気工事士筆記試験(問6)』
解説
正解は「ロ.70」です。
この問題のポイントは、tanθを使って計算する事です。
設置する進相コンデンサの容量を求められているので、力率改善前と改善後の無効電力の差し引きが答えになります。
tanθを使うと早く計算ができます。使わなくても答えは求められます。tanθを使う方法を①に、使わない方法を②で解説します。

自分に合った計算方法を覚えておこう!
解き方①
tanθを使って計算する方法です。
無効電力を求める
力率改善前と改善後の無効電力を求めます。
tanθが示されているので、それを使って求めます。tanθは次の式で表せます。
\(tanθ=\Large{\frac{無効電力Q}{消費電力P}}\)これを使って無効電力Qを求めると、次のようになります。
\(Q=Ptanθ\)力率改善前の無効電力をQ1、力率改善後の無効電力をQ2とし,それぞれを求めます。
\(Q_1=120\times1.33\) \(Q_2=120\times0.75\)ここで計算してもいいですが、後の計算が楽になるのでこのままにしておきます。
進相コンデンサの容量を求める
力率改善の為の進相コンデンサの容量は、無効電力の差し引きで求められます。
\(Q=Q_1-Q_2\\~~~=(120\times1.33)-(120\times0.75)\\~~~=120\times(1.33-0.75)\\~~~=120\times0.58\\~~~=69.6[kvar]\)計算の答えは69.6[kvar]なので、答えは70[kvar]となります。
解き方②
tanθを使わない方法です。
力率改善前の無効電力を求める
力率改善前の無効電力Q1を求めます。
無効電力は次の式で求められます。無効電力をQ、定格容量をS、消費電力をPとします。
\(Q_1=\sqrt{S^2-P^2}\\~~~~~=\sqrt{200^2-120^2}\\~~~~~=\sqrt{40000-14400}\\~~~~~=\sqrt{25600}\\~~~~~=160[kvar]\)力率改善後の無効電力を求める
力率改善後の無効電力Q2を求めます。
力率cosθ2と消費電力Pより、力率改善後の定格容量S2を求まます。
力率cosθは次の式が成り立ちます。
\(cosθ=\Large{\frac{消費電力P}{定格容量S}}\)これから定格容量S2を求まます。
\(S_2=\Large{\frac{P}{cosθ_2}}\\~~~~~=\Large{\frac{120}{0.8}}\\~~~~~=150[kV・A]\)求めたS2を使って、無効電力Q2を求めます。
\(Q_2=\sqrt{S_2^2-P^2}\\~~~~~=\sqrt{150^2-120^2}\\~~~~~=\sqrt{22500-14400}\\~~~~~=\sqrt{8100}\\~~~~~=90[kvar]\)進相コンデンサの容量を求める
力率改善の為の進相コンデンサの容量は、無効電力の差し引きで求められます。
\(Q=Q_1-Q_2\\~~~=160-90\\~~~=70[kvar]\)よって答えは70[kvar]となります。






















コメント