【2019年度】第一種電気工事士《筆記試験》問2

問題

図の直流回路において，抵抗3Ωに流れる電流I3の値[A] は。

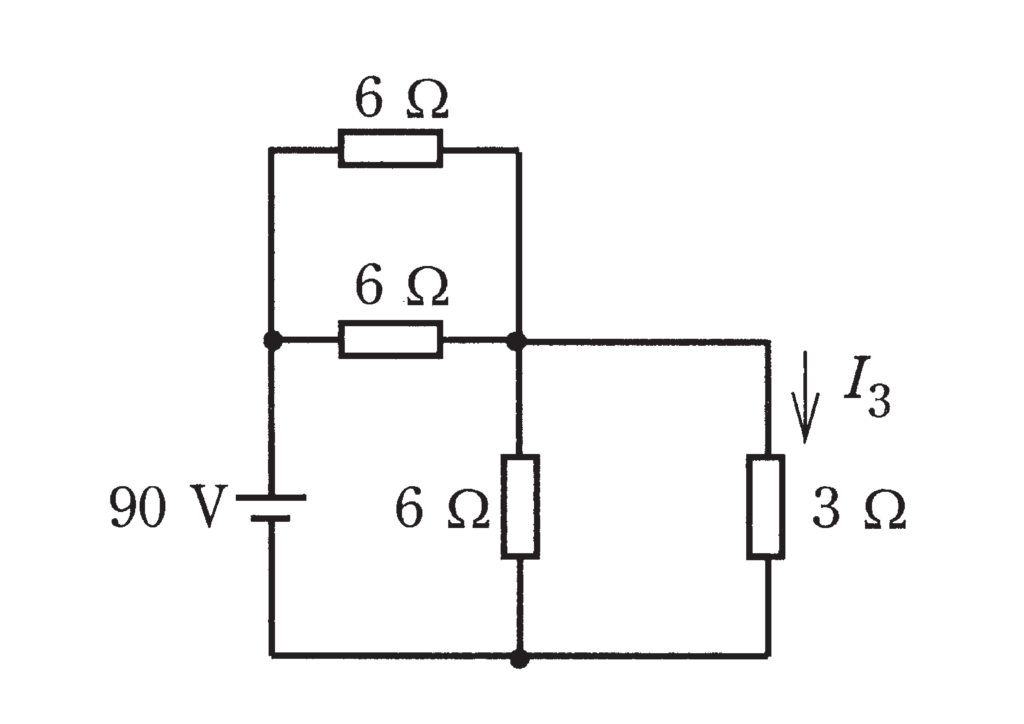
答え

イ．3

ロ．9

ハ．12

ニ．18

『出典：2019年度第一種電気工事士筆記試験(問2)』

解説

正解は「ハ．12」です。

この問題のポイントは、回路図を分かりやすいように変換する事です。ぱっと見は複雑な回路図ですが、実は普通の回路図です。そこに気付けるかが問題です。

回路図を分かりやすくする

まず問題の回路図を分かりやすいように変換します。次のような形になります。

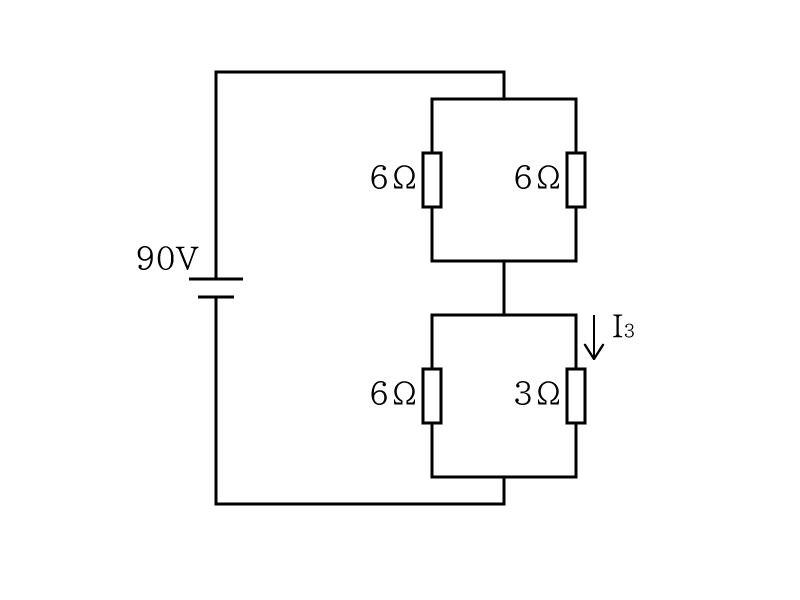
これに気付けるかが、この問題のポイントになります。変換する時のポイントは問題の図の●の接続点を起点に考えることです。

この図を使って解いていきます。

解き方

並列接続部を合成する

問題の回路図には、2つの並列接続された抵抗が直列に接続されています。まず並列接続された抵抗をそれぞれ合成します。上側の抵抗をR1、下側をR2とします。

\(R_1＝\Large{\frac{6\times6}{6+6}}\\~~~~＝\Large{\frac{36}{12}}\\~~~~＝3[Ω]\)

\(R_2＝\Large{\frac{6\times3}{6+3}}\\~~~~＝\Large{\frac{18}{9}}\\~~~~＝2[Ω]\)

問題の部分にかかる電圧を計算する

先ほど求めた抵抗からR2にかかる電圧を求めます。分圧の式を使うと次のようになります。

\(V_2＝\Large{\frac{R_2}{R_1+R_2}}\normalsize{V}\\~~~~＝\Large{\frac{2}{3+2}}\normalsize{\times90}\\~~~~＝36[V]\)

並列回路にかかる電圧は等しいことから、問題の電流I3が流れる3Ωの抵抗にかかる電圧は36[V]と分かります。

電流I3を求める

先ほど求めた電圧より電流I3を求めます。

\(I_3＝\Large{\frac{V}{R}}\\~~~~＝\Large{\frac{36}{3}}\\~~~~＝12[A]\)