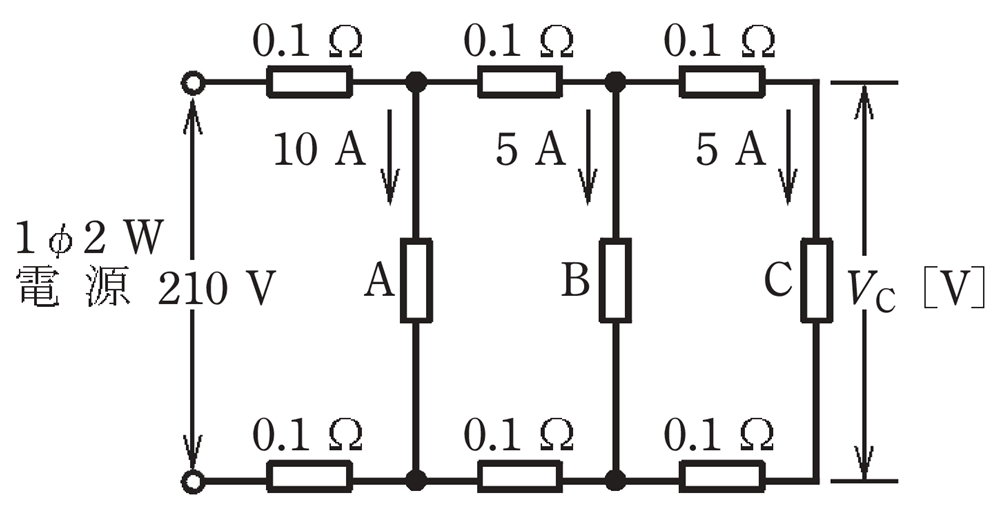
図のように,単相2線式の配電線路で,抵抗負荷A,B,Cにそれぞれ負荷電流10A,5A,5Aが流れている。電源電圧が210Vであるとき,抵抗負荷Cの両端の電圧VC[V]は。
ただし,電線1線当たりの抵抗は0.1Ωとし,線路リアクタンスは無視する。
答え
イ.201
ロ.203
ハ.205
ニ.208
『出典:令和4年度第一種電気工事士筆記試験【午前】(問6)』
解説
正解は「ロ.203」です。
この問題のポイントは、配電線路の電圧降下についてです。
単相2線式の電圧降下は次の式で求められます。
\(v=2Ir\)
ただし、この問題では各ポイントで流れる電流が違うので注意です。

ボルベア
各ポイントに流れる電流の大きさに注意!
解き方
各ポイントの電流を考える
問題では各抵抗負荷A,B,Cに流れる電流が示されています。しかし配電線路に流れる電流は各ポイントで合計する必要があります。
抵抗負荷Cの手前の電線抵抗0.1Ωに流れる電流となります。
抵抗負荷Bの手前の電線抵抗0.1Ωに流れる電流は、抵抗負荷Bの5Aと抵抗負荷Cの5Aを合計した10Aとなります。
抵抗負荷Aの手前の電線抵抗0.1Ωに流れる電流は、抵抗負荷Aの10Aと抵抗負荷Bの5Aと抵抗負荷Cの5Aを合計した20Aとなります。
各ポイントの電圧降下を求める
各電線の抵抗毎に流れる電流が違うので、それぞれで電圧降下vを求める必要があります。
\(v_A=2Ir\\~~~~=2\times20\times0.1\\~~~~=4[V]\)
\(v_B=2Ir\\~~~~=2\times10\times0.1\\~~~~=2[V]\)
\(v_C=2Ir\\~~~~=2\times5\times0.1\\~~~~=1[V]\)
VCを求める
各ポイントの電圧降下の値が分かったので、電源電圧から各電圧降下を引けばVCの電圧となります。
\(V_C=V-v_A-v_B-v_C\\~~~~~=210-4-2-1\\~~~~~=203[V]\)






















コメント