【2018年度】第一種電気工事士《筆記試験》問6

問題

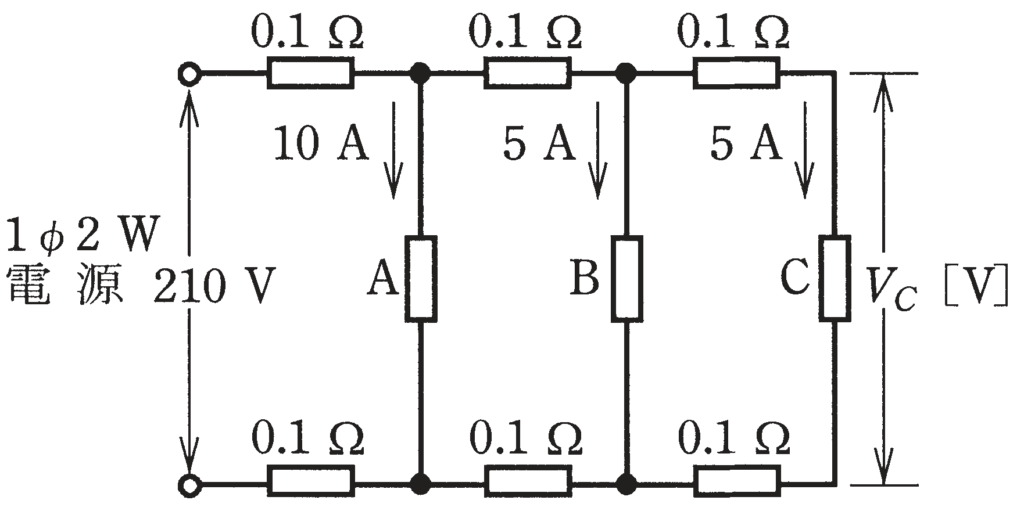
図のように，単相2線式の配電線路で，抵抗負荷A,B,Cにそれぞれ負椅電流10A,5A,5Aが流れている。電源電圧が210Vであるとき，抵抗負荷Cの両端の電圧VC[V]は。
ただし，電線1線当たりの抵抗は0.1Ωとし，線路リアクタンスは無視する。

答え

イ．201

ロ．203

ハ．205

ニ．208

『出典：平成30年度第一種電気工事士筆記試験(問6)』

解説

正解は「ロ．203」です。

この問題のポイントは、それぞれのポイントにおける電流値に注意する事です。

計算自体は簡単ですが、電流の流れを意識してそれぞれに流れる電流値を求めて計算しましょう。

解き方

各ポイントの電流値を考える

まず各線路抵抗に流れる電流を求めます。

各線路抵抗を左から「r1・r2・r3」とします。

r1に流れる電流は、負荷A、B、Cに流れる電流の合計になります。よって次の式のようになります。

\(I_{r1}=10+5+5\\~~~~~~=20[A]\)

r2に流れる電流は、負荷B、Cに流れる電流の合計になります。よって次の式のようになります。

\(I_{r2}=5+5\\~~~~~~=10[A]\)

r3に流れる電流は、負荷Cに流れる電流になります。よって次のようになります。

\(I_{r3}=5[A]\)

それぞれの電圧降下を求める

単相2線式における電圧降下VLは次の式で求められます。

\(V_L=2Ir[V]\)

r1の電圧降下は次の式で求められます。

\(V_{L1}=2I_{r1}r_1\\~~~~~~=2\times20\times0.1\\~~~~~~=4[V]\)

r2の電圧降下は次の式で求められます。

\(V_{L2}=2I_{r2}r_2\\~~~~~~=2\times10\times0.1\\~~~~~~=2[V]\)

r3の電圧降下は次の式で求められます。

\(V_{L3}=2I_{r3}r_3\\~~~~~~=2\times5\times0.1\\~~~~~~=1[V]\)

VCを求める

先ほど求めた電圧降下から問題のVCを求めます。

電源電圧からそれぞれの電圧降下を引くとVCを求めることができます。

\(V_C=V-(V_{L1}+V_{L2}+V_{L3})\\~~~~=210-(4+2+1)\\~~~~=210-7\\~~~~=203[V]\)