【令和2年度】第一種電気工事士《筆記試験》問2

問題

図のような直流回路において， a-b間の電圧[V]は。

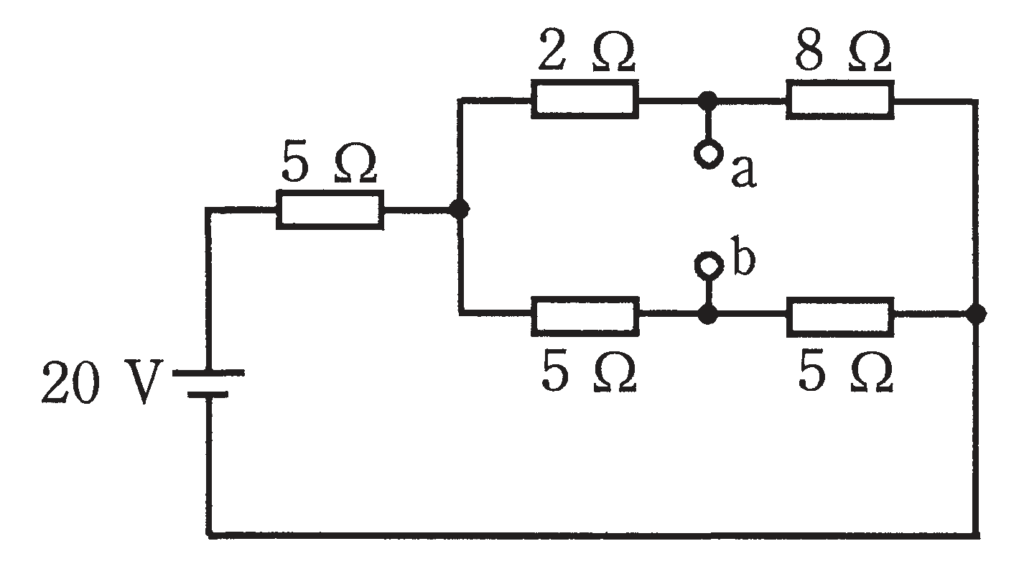
答え

イ．2

ロ．3

ハ．4

ニ．5

『出典：令和2年度第一種電気工事士筆記試験(問2)』

解説

正解は「ロ．3」です。

この問題では、a-b間の電圧を求めます。

その為には、回路右側にある8[Ω]と5[Ω]それぞれにかかる電圧を計算し、その差が答えになります。

解き方

回路右側の抵抗を合成する

回路右側の4個の抵抗の直並列回路を1つの抵抗に合成します。これをRxとします。

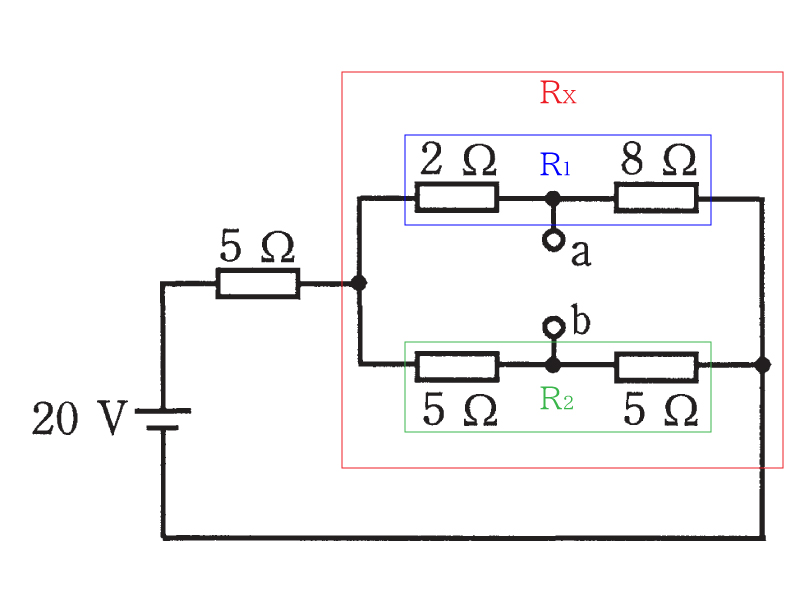
まず直列部分の上側をR1、下側をR2として合成すると、次のようになります。

\(R_1=2+8\\~~~~=10[Ω]\)

\(R_2=5+5\\~~~~=10[Ω]\)

どちらも10[Ω]になることがわかります。

このR1とR2の並列回路を「和分の積」を使って合成すると、次のようになります。

\(R_x=\Large{\frac{R_1R_2}{R_1+R_2}}\\~~~~=\Large{\frac{10\times10}{10+10}}\\~~~~=\Large{\frac{100}{20}}\\~~~~=5[Ω]\)

回路右側にかかる電圧を求める

先程の計算より回路全体で、5[Ω]と5[Ω]の直列回路が出来上がりました。同じ抵抗値なので、電圧は等しく分圧されることがわかります。すると右側の抵抗Rx部分には10[V]がかかっている事がわかります。

各所の電圧を求める

次に回路を初期のように戻して、右側部分に10[V]を当てはめて考えていきましょう。

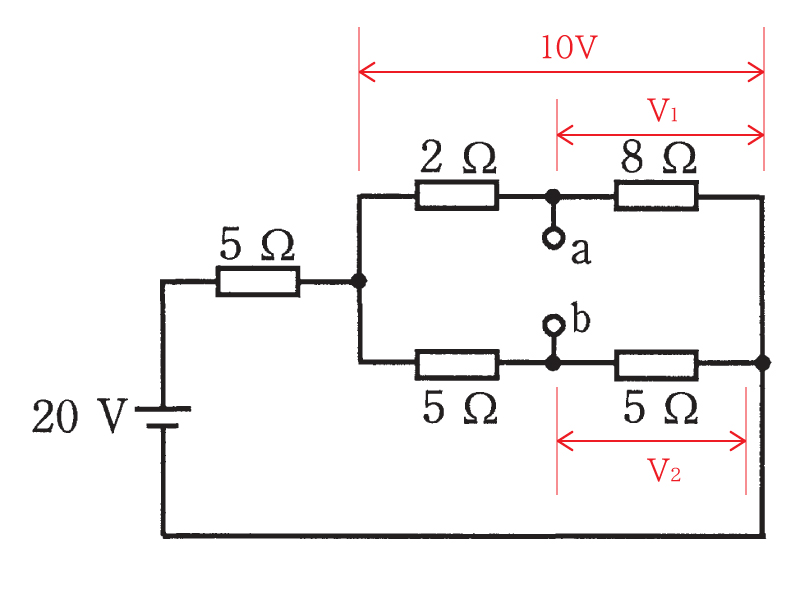
ここから右側上部の8[Ω]と右側下部の5[Ω]にかかる電圧V1とV2を求めていきます。

分圧の式よりそれぞれ次のようになります。

\(V_1=\Large{\frac{8}{2+8}}\normalsize{V}\\~~~~=\Large{\frac{8}{10}}\normalsize{\times10}\\~~~~=8[V]\)

\(V_2=\Large{\frac{5}{5+5}}\normalsize{V}\\~~~~=\Large{\frac{5}{10}}\normalsize{\times10}\\~~~~=5[V]\)

a-b間の電圧を求める

a-b間の電圧はこのV1とV2の差なので次のようになります。

\(V_{ab}=V_1-V_2\\~~~~=8-5\\~~~~=3[V]\)