問題
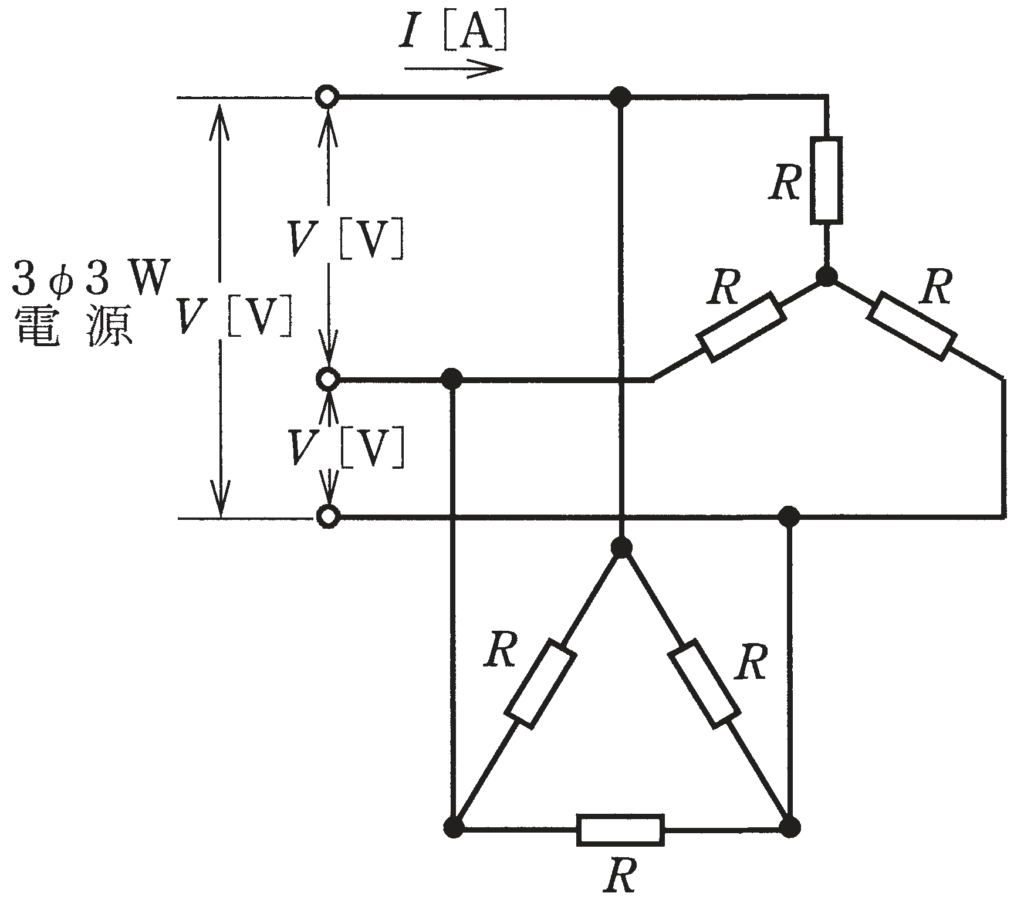
図のように,線間電圧V[V]の三相交流電源から, Y 結線の抵抗負荷とΔ結線の抵抗負荷に電力を供給している電路がある。図中の抵抗RがすべてR[Ω]であるとき,図中の電路の線電流I[A]を示す式は。
答え
イ.\(\Large{\frac{V}{R}}\Large{(\frac{1}{\sqrt{3}}}\normalsize{+1}\Large{)}\)
ロ.\(\Large{\frac{V}{R}}\Large{(\frac{1}{2}}\normalsize{+\sqrt{3}}\Large{)}\)
ハ.\(\Large{\frac{V}{R}}\Large{(\frac{1}{\sqrt{3}}}\normalsize{+\sqrt{3}}\Large{)}\)
ニ.\(\Large{\frac{V}{R}}\Large{(}\normalsize{2}+\Large{\frac{1}{\sqrt{3}})}\)
『出典:平成30年度第一種電気工事士筆記試験(問5)』
解説
正解は「ハ.\(\Large{\frac{V}{R}}\Large{(\frac{1}{\sqrt{3}}}\normalsize{+\sqrt{3}}\Large{)}\)」です。
この問題のポイントは、Y結線とΔ結線に流れる線電流を別々に計算する事です。
Y結線に流れる線電流とΔ結線に流れる線電流をそれぞれ計算し、それを足したものが答えになります。

それぞれの電流を求めよう!
解き方
Y結線に流れる線電流を求める
Y結線の部分に流れる線電流を求めます。
Y結線の抵抗Rにかかる電圧は\(\Large{\frac{V}{\sqrt{3}}}\)になります。よって電流IYは次の式で示すことができます。
\(I_Y=\Large{\frac{\frac{V}{\sqrt{3}}}{R}}\\~~~~=\Large{\frac{V}{\sqrt{3}R}}\)Y結線では相電流は線電流と等しいので、上記のIYがY結線の線電流となります。
また問題の答えでは\(\Large{\frac{V}{R}}\)でまとめてあるので、それに合う形に変換しておきます。
\(I_Y=\Large{\frac{V}{\sqrt{3}R}}\\~~~~=\Large{\frac{V}{R}}\normalsize{\times}\Large{\frac{1}{\sqrt{3}}}\)Δ結線に流れる線電流を求める
Δ結線の部分に流れる線電流を求めます。
Δ結線の抵抗Rにかかる電圧は線間電圧と同じになりVとなります。よって相電流IΔは次の式で示すことができます。
\(I_Δ=\Large{\frac{V}{R}}\)しかしΔ結線の線電流は、相電流の\(\sqrt{3}\)倍となるので、線電流IΔは次のように示すことができます。
\(I_Δ=\sqrt{3}\Large{\frac{V}{R}}\)また問題の答えでは\(\Large{\frac{V}{R}}\)でまとめてあるので、それに合う形に変換しておきます。
\(I_Δ=\sqrt{3}\Large{\frac{V}{R}}\\~~~~=\Large{\frac{V}{R}}\normalsize{\times}\sqrt{3}\)それぞれの線電流を合わせる
電流IYとIΔを足したものが答えになります。
\(I=I_Y+I_Δ\\~~=\Large{\frac{V}{R}}\normalsize{\times}\Large{\frac{1}{\sqrt{3}}}\normalsize{+}\Large{\frac{V}{R}}\normalsize{\times}\sqrt{3}\\~~=\Large{\frac{V}{R}}\Large{(\frac{1}{\sqrt{3}}}\normalsize{+\sqrt{3}}\Large{)}\)





















コメント