【令和4年度（午後）】第一種電気工事士《筆記試験》問6

2022年度（令和4年度）午後
当サイトはアフェリエイト広告を利用しています。
スポンサーリンク

問題

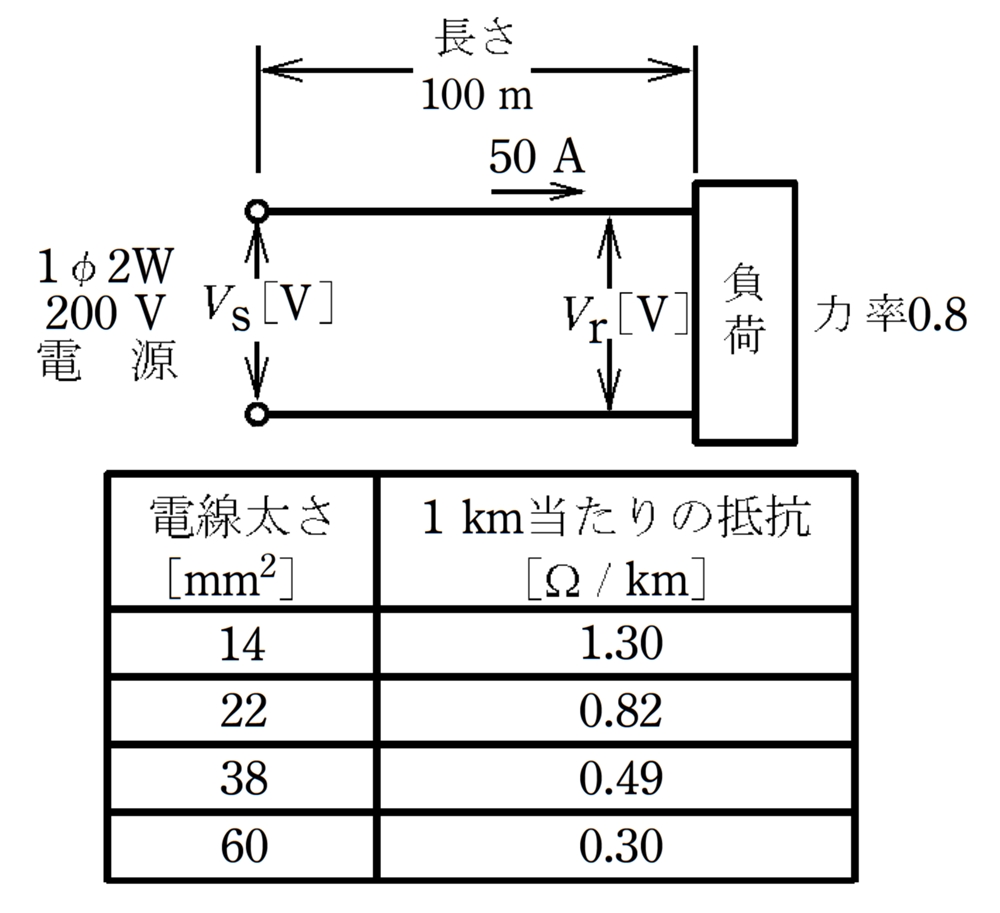
図のような単相2線式配電線路において，配電線路の長さは100m，負荷は電流50A，力率0.8（遅れ）である。線路の電圧降下（Vs-Vr）［V］を4V以内にするための電線の最小太さ（断面積）［㎟］は。
ただし，電線の抵抗は表のとおりとし，線路のリアクタンスは無視するものとする。

答え

イ．14

ロ．22

ハ．38

ニ．60

『出典：令和4年度第一種電気工事士筆記試験【午後】（問6）』

スポンサーリンク

解説

正解は「ハ．38」です。

この問題のポイントは、電圧降下についてです。

この問題ではただ単に電圧降下を求めるだけではなく、そこから電線の太さを求めなければいけません。

各単位に注意しましょう。

ボルベア
ボルベア

電線の太さを求めよう！

解き方

抵抗Rを求める

電圧降下は4V以内とされているので、電圧降下の式から抵抗Rを求めます。

本来の単相2線式の電圧降下の式は次の通りです。

\(V_s-V_r=2I(R\cos\theta+x\sin\theta)\)

しかし今回がリアクタンスXは無視するとあるので、次の式となります。

\(V_s-V_r=2IR\cos\theta\)
\(V_s-V_r=2IR\cos\theta\\~~~~~~~~~~R=\Large{\frac{V_s-V_r}{2I\cos\theta}}\\~~~~~~~~~~~~~=\Large{\frac{4}{2\times50\times0.8}}\\~~~~~~~~~~~~~=0.05［Ω］\)

抵抗Rが求められたので電圧降下を4V以内にするには、抵抗Rが0.05Ω以内でなければいけません。

電線の太さを求める

先ほどの計算から、抵抗Rは0.05Ω以下でなければいけないことが分かりました。

表の各電線太さは1㎞当たりなので、問題の回路の100ｍに換算します。

  • 14㎟＝1.30×0.1＝0.130［Ω］
  • 22㎟＝0.82×0.1＝0.082［Ω］
  • 38㎟＝0.49×0.1＝0.049［Ω］
  • 60㎟＝0.30×0.1＝0.030［Ω］

0.05Ω以下となるのは38㎟と60㎟になりますが、問題では最小の太さを問われているので、38㎟が答えとなります。

スポンサーリンク

コメント