【令和6年度】第一種電気工事士《筆記試験》問8

2024年度（令和6年度）
当サイトはアフェリエイト広告を利用しています。
スポンサーリンク

問題

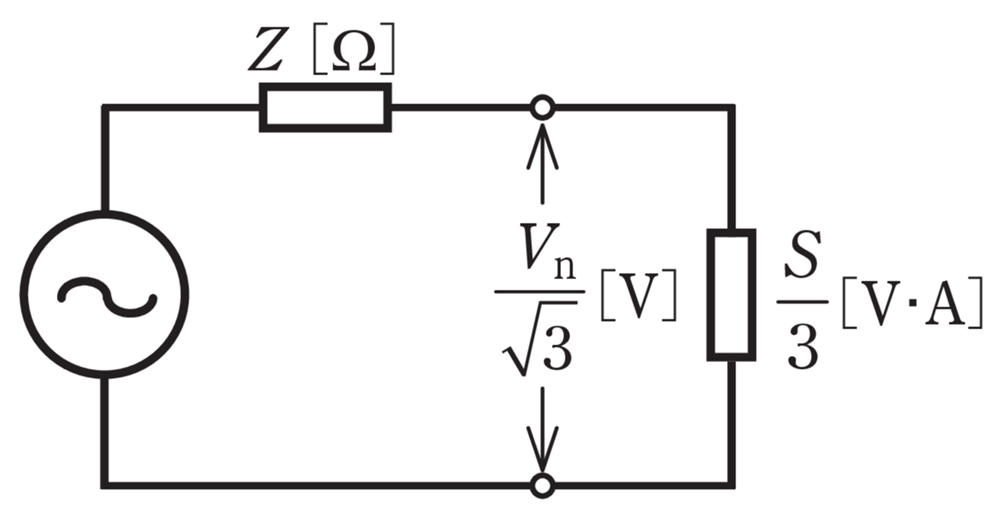
定格一次電圧がVn［V］，定格容量がS［V･A］，一次側に換算した変圧器の内部インピーダンスがZ［ Ω］（1相分）の三相変圧器がある。この変圧器の百分率インピーダンス％Z［％］（基準容量S［V･A］）を示す式は。

ただし，図は 1 相分の等価回路を示す。

答え

イ．\(％Z=\Large{\frac{ZS}{V_n}}\normalsize{\times100}\)

ロ．\(％Z=\Large{\frac{V_n}{ZS}}\normalsize{\times100}\)

ハ．\(％Z=\Large{\frac{ZS}{{V_n}^{2}}}\normalsize{\times100}\)

ニ．\(％Z=\Large{\frac{ZS^{2}}{V_n}}\normalsize{\times100}\)

『出典：令和6年度第一種電気工事士筆記試験（問8）』

スポンサーリンク

解説

正解は「ハ．\(％Z=\Large{\frac{ZS}{{V_n}^{2}}}\normalsize{\times100}\)」です。

この問題のポイントは、変圧器の百分率インピーダンスについてです。

変圧器の百分率インピーダンス％Zとは、定格電圧Vnに対する内部インピーダンスZによる電圧降下の割合を表したものです。

内部インピーダンスZによる電圧降下は定格電流Inを使用して、ZInで表せます。

これらをまとめると次の式となります。

\(％Z=\Large{\frac{ZI_n}{V_n}}\normalsize{\times100}［％］\)

第一種電気工事士試験の中では難しい部類の問題です。あまり出題されない問題ですので、余裕があれば覚えておきましょう。

ボルベア
ボルベア

百分率インピーダンスについて理解しよう！

解き方

基本の式

変圧器の百分率インピーダンス％Zは、先ほど説明した通り次の式で表せます。

\(％Z=\Large{\frac{ZI_n}{V_n}}\normalsize{\times100}［％］…①\)

基準容量Sを表す式

次に基準容量Sを表す式を考えます。

基準容量S［V･A］は定格電圧×定格電流で表せます。

\(S={V}_n{I}_n［V･A］…②\)

式をまとめる

問題では基準容量Sを使用して、変圧器の百分率インピーダンス％Zを表しています。

これまでに示した式２つを見ると式①にVn/Vnを追加すれば、式をまとめることができます。

\(％Z=\Large{\frac{ZI_n}{V_n}}\normalsize{\times100}\\~~~~~~=\Large{\frac{ZI_n}{V_n}}\normalsize{\times100\times\Large{\frac{V_n}{V_n}}}\\~~~~~~=\Large{\frac{Z{I}_n{V}_n}{{V}_n^{2}}}\normalsize{\times100}\\~~~~~~=\Large{\frac{ZS}{{V}_n^{2}}}\normalsize{\times100}\)

スポンサーリンク

コメント