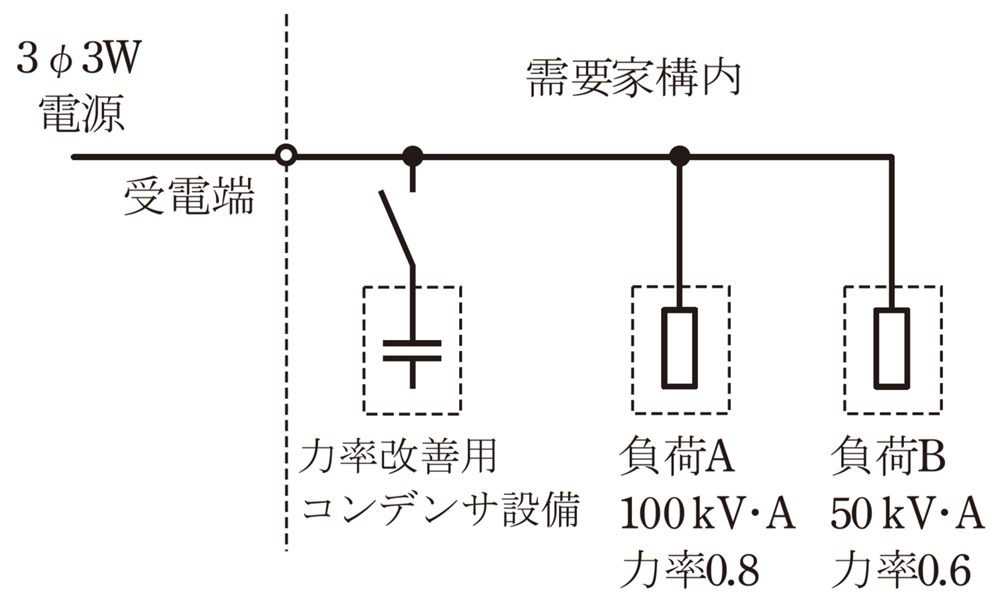
図のように,三相3 線式高圧配電線路の末端に,負荷容量100kV・A( 遅れ力率0.8)の負荷A と,負荷容量50kV・A(遅れ力率0.6)の負荷Bに受電している需要家がある。
需要家全体の合成力率(受電端における力率)を1にするために必要な力率改善用コンデンサ設備の容量[kvar]は。
答え
イ.40
ロ.60
ハ.100
ニ.110
『出典:令和5年度第一種電気工事士筆記試験【午前】(問9)』
解説
正解は「ハ.100」です。
この問題のポイントは、回路の力率改善についてです。
力率改善の問題としては少し複雑ですが、考え方さえ覚えておけば簡単に解ける問題です。

ボルベア
力率改善は全体の無効電力で考える!
解き方
負荷Aと負荷Bの無効電力を求める
負荷Aと負荷Bそれぞれの無効電力を求めます。
まずは負荷容量Sと力率から消費電力Pを求めます。
\(P_A=S_A\cos\theta\\~~~~~~=100\times0.8\\~~~~~~=80[kW]\)
\(P_B=S_B\cos\theta\\~~~~~~=50\times0.6\\~~~~~~=30[kW]\)
次に負荷容量Sと消費電力Pから、無効電量Qを求めます。
\(Q_A=\sqrt{{S_A}^{2}-{P_A}^{2}}\\~~~~~~=\sqrt{{100}^{2}-{80}^{2}}\\~~~~~~=\sqrt{3600}\\~~~~~~=60[kvar]\)
\(Q_B=\sqrt{{S_B}^{2}-{P_B}^{2}}\\~~~~~~=\sqrt{{50}^{2}-{30}^{2}}\\~~~~~~=\sqrt{1600}\\~~~~~~=40[kvar]\)
コンデンサの容量を求める
問題で求められている需要家全体の力率を1にするには、負荷Aと負荷Bの無効電力を合計したものと同じ容量のコンデンサを設置する必要があります。
よって下記の式で求められます。
\(コンデンサ容量=Q_A+Q_B\\~~~~~~~~~~~~~~~~~~~~~~=60+40\\~~~~~~~~~~~~~~~~~~~~~~=100[kvar]\)






















コメント