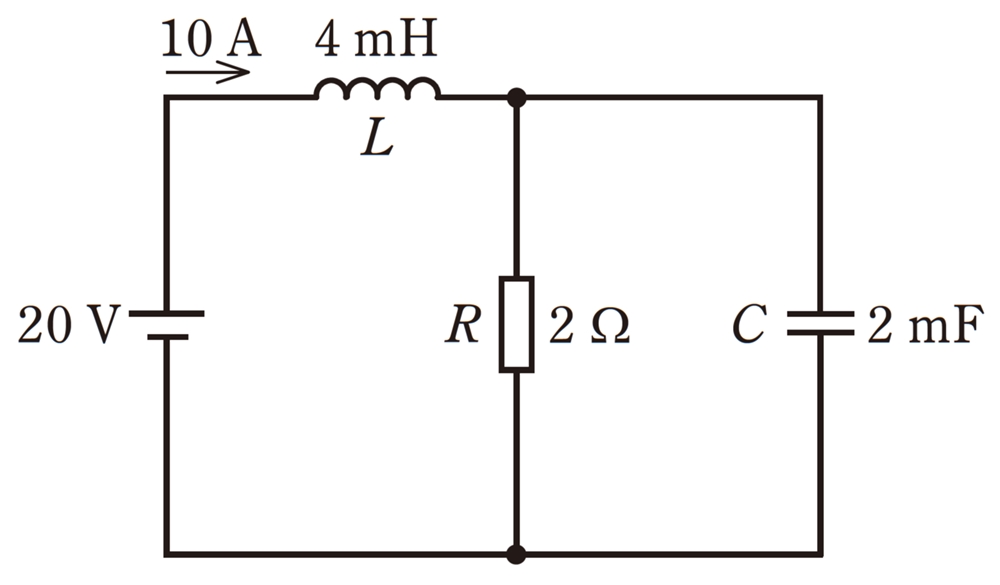
図のような直流回路において,電源電圧20V,R=2Ω,L=4mH及びC=2mFで,RとLに電流10Aが流れている。Lに蓄えられているエネルギーWL[J]の値と,Cに蓄えられているエネルギーWC[J]の値の組合せとして,正しいものは。
答え
イ.WL=0.2 WC=0.4
ロ.WL=0.4 WC=0.2
ハ.WL=0.6 WC=0.8
ニ.WL=0.8 WC=0.6
『出典:令和5年度第一種電気工事士筆記試験【午前】(問1)』
解説
この問題のポイントは、コイルとコンデンサのエネルギーの公式と、直流回路におけるコイルとコンデンサの扱いです。
コイルのエネルギーの公式…
\(W_L=\Large{\frac{1}{2}}\normalsize{LI^{2}}\)コンデンサのエネルギーの公式…
\(W_C=\Large{\frac{1}{2}}\normalsize{CV^{2}}\)コイルとコンデンサに蓄えられるエネルギーの公式については、こちらで詳しく解説しています。

ボルベア
コイルとコンデンサのエネルギーの公式を覚えておこう!
解き方
コイルのエネルギーを求める
コイルに蓄えられるエネルギーを求めるには、コイルに流れる電流が必要です。
電流は、問題から10Aであることが分かります。
よって次の式で求められます。
\(W_L=\Large{\frac{1}{2}}\normalsize{LI^{2}}\\~~~~~~=\Large{\frac{1}{2}}\normalsize{\times4\times10^{-3}\times10^{2}}\\~~~~~~=2\times10^{-1}\\~~~~~~=0.2[J]\)
コンデンサのエネルギーを求める
コンデンサに蓄えられるエネルギーを求めるには、コンデンサにかかる電圧が必要です。
コイルが直列に接続されていますが、直流回路においてはコイルは短絡とみなせるので無視できます。よって図からコンデンサにかかる電圧は20Vと分かります。
よって次の式で求められます。
\(W_C=\Large{\frac{1}{2}}\normalsize{CV^{2}}\\~~~~~~=\Large{\frac{1}{2}}\normalsize{\times2\times10^{-3}\times20^{2}}\\~~~~~~=400\times10^{-3}\\~~~~~~=0.4[J]\)























コメント