電気工事士試験の基本となるのがオームの法則です。オームの法則を駆使して計算問題を解いていきます。
オームの法則の要素の1つに抵抗があります。電気工事士試験では、回路全体の合成抵抗を求めてから、回路全体の電流を求めたりする問題があります。
そこで知っておくべきなのが、合成抵抗の計算です。
ここでは合成抵抗の公式について解説します。
合成抵抗の公式
合成抵抗とは、複数の抵抗を1つの抵抗と見なすことです。
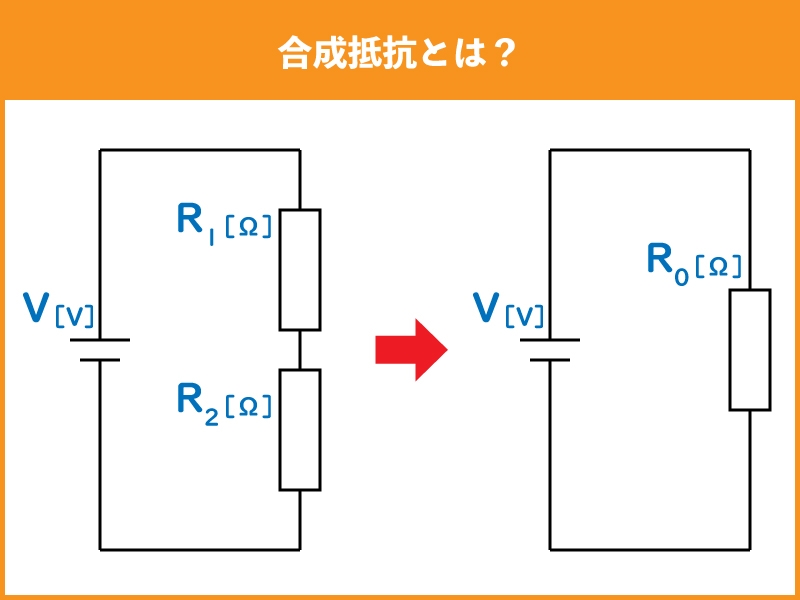
これを活用して回路全体の合成抵抗と電源電圧からオームの法則を使い、回路全体の電流を求めたりします。
合成抵抗の公式は合成する抵抗の接続によって変わり、2つの種類に分けられます。
それぞれの場合に分けて解説します。
直列接続の場合
下記のような直列に接続された抵抗の合成抵抗は、どの様に求めるでしょうか。
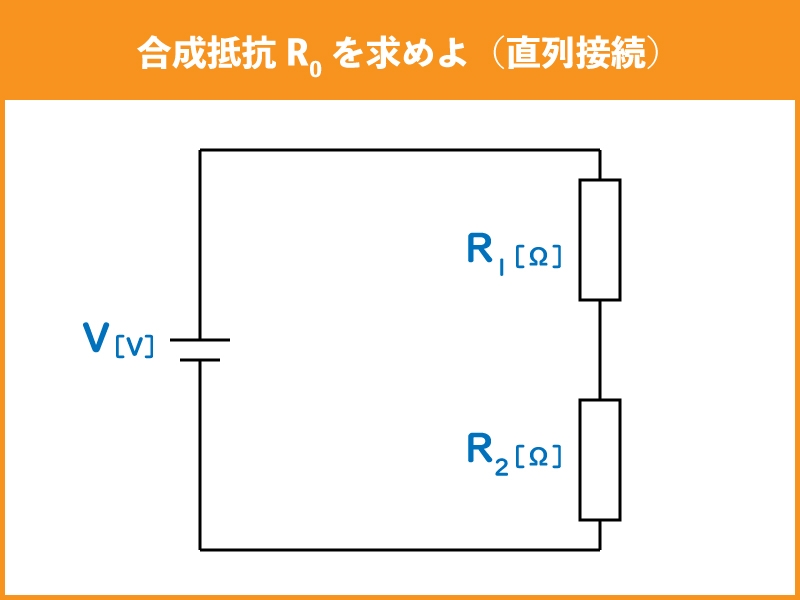
直列接続された抵抗を合成する場合は、下記の公式で導くことができます。
(直列接続の場合)
\(R_{0}=R_{1}+R_{2}[Ω]\)
このように直列に接続された抵抗は、単純に足算をすれば合成抵抗を求められます。
例題では抵抗が2つの場合ですが、3つ以上の場合でも足算をしていけば良いです。
並列接続の場合
並列接続の場合は、いくつかの方法で合成抵抗を求めることができます。
状況によって使い分けをしましょう。
基本
まずは並列接続されている抵抗の合成抵抗を求める、基本の公式について解説します。
下記のような並列に接続された抵抗の合成抵抗は、どの様に求めるでしょうか。
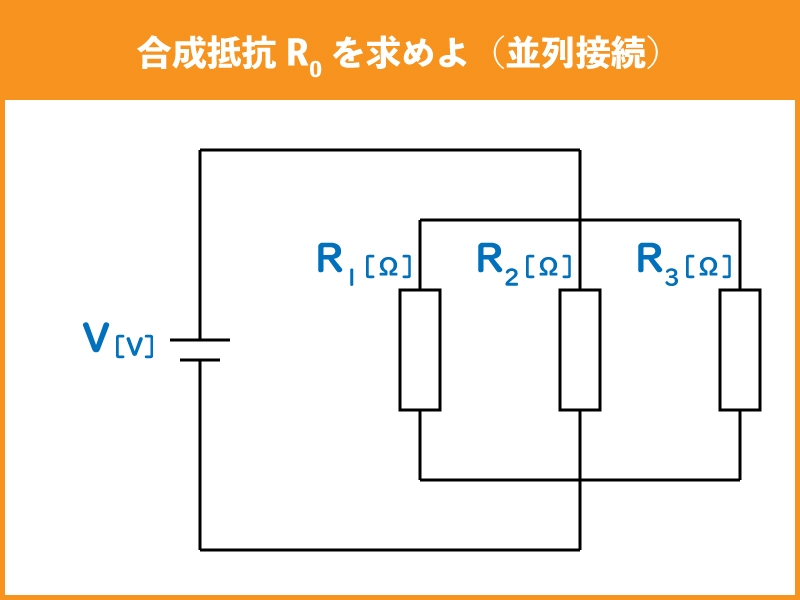
並列接続された抵抗を合成する場合は、下記の公式で導くことができます。
(並列接続の場合)
\(R_{0}=\Large{\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}}}\normalsize{[Ω]}\)
このように並列に接続された抵抗は、逆数を足していく方法で求められます。直列に比べて複雑な計算となります。
例題では抵抗が3つの場合ですが、2つでも4つ以上の場合でも同様に求められます。
2個の場合(和分の積)
次に並列接続の抵抗が2つの場合に限り、適用できる公式を解説します。
下記のような並列に接続された抵抗の合成抵抗は、どの様に求めるでしょうか。
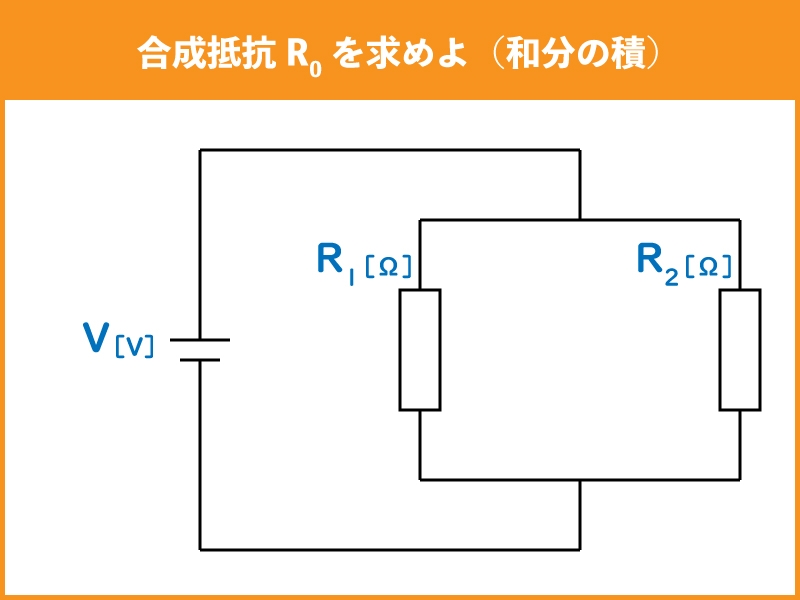
並列接続された抵抗が2つの場合は、下記の公式で導くことができます。
(和分の積)
\(R_{0}=\Large{\frac{R_{1}\times{R_{2}}}{R_{1}+R_{2}}}\normalsize{[Ω]}\)
この公式を「和分の積」と言います。2つの抵抗の積(×)を和(+)で除算(÷)している(積/和)ことから、この名称となっています。
並列接続の基本の式より簡単に合成抵抗を求められるので、よく使う式です。
しかし、この式は抵抗が2つの場合しか使用できません。3つの場合は、まず2つの抵抗を和分の積で合成して、その合成抵抗と残った1つの抵抗を和分の積で合成すれば全体の合成抵抗となります。
順々に2つの抵抗を合成していくことで、2つ以上の抵抗も合成することも可能です。
同じ値の抵抗を合成する場合
並列接続する抵抗が全て同じ値の場合には、さらに簡単に合成抵抗を求められます。
2つの抵抗なら1つの抵抗の1/2、3つなら1/3となります。
4Ωの抵抗が2つ並列接続されている場合は、合成抵抗は2Ωとなります。
9Ωの抵抗が3つ並列接続されている場合は、合成抵抗は3Ωとなります。
これまでの公式を使っても同様の結果とありますが、このテクニックを覚えておけば計算時間を短縮できます。
練習問題
合成抵抗の公式を解説しました。
ここからは公式を使って、練習問題を解いていきます。
例題1
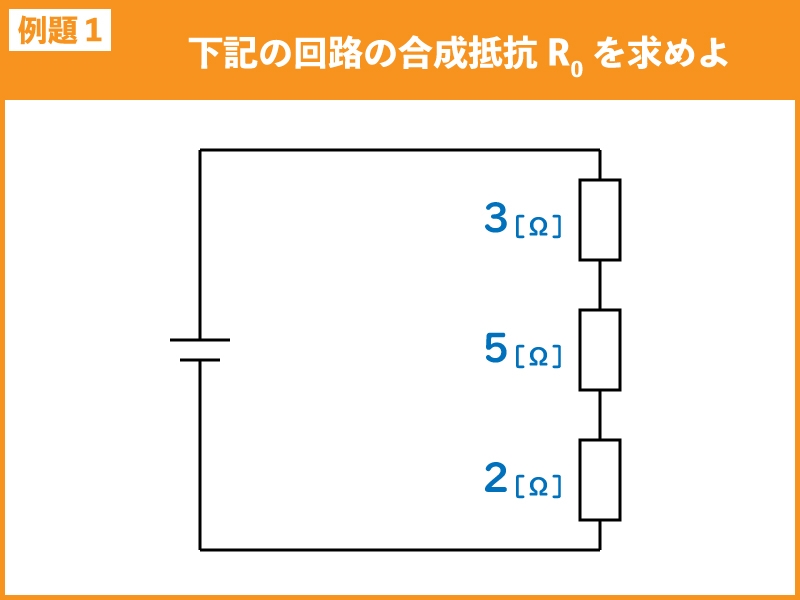
下記の回路の合成抵抗R0を求めよ。
解説
例題1は、直列接続なので下記のとおり求められます。
\(R_{0}=R_{1}+R_{2}+R_{3}\\~~~~~=3+5+2\\~~~~~=10[Ω]\)
例題2
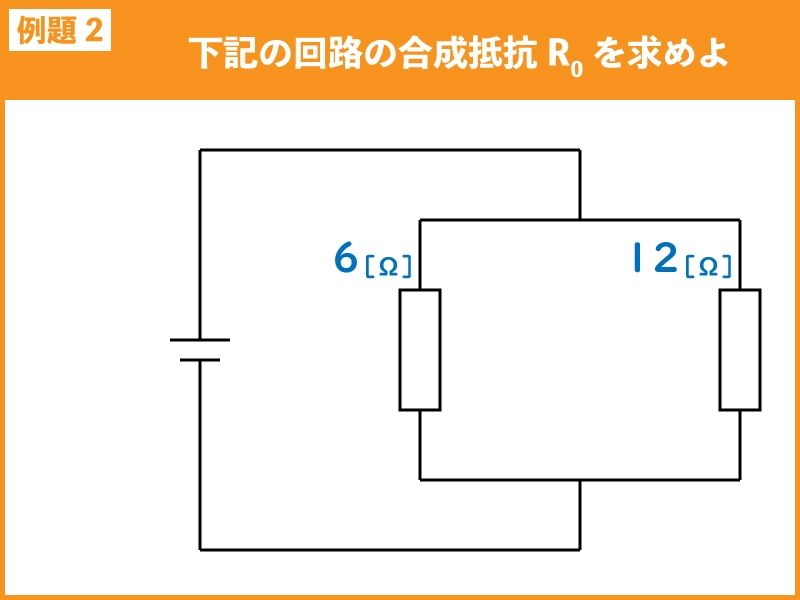
下記の回路の合成抵抗R0を求めよ。
解説
例題2は2個の並列接続なので、和分の積を使って求めます。
\(R_{0}=\Large{\frac{R_{1}\times{R_{2}}}{R_{1}+R_{2}}}\\~~~~~=\Large{\frac{6\times12}{6+12}}\\~~~~~=\Large{\frac{72}{18}}\\~~~~~=4[Ω]\)
例題3
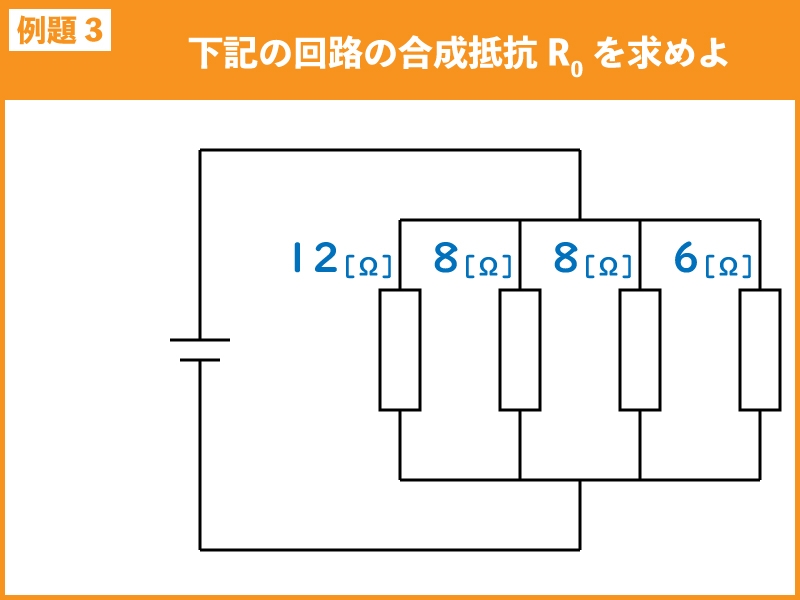
下記の回路の合成抵抗R0を求めよ。
解説
例題3は4個の並列接続なので、並列接続の基本式を使って求めます。
\(R_{0}=\Large{\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4}}}\\~~~~~=\Large{\frac{1}{\frac{1}{12}+\frac{1}{8}+\frac{1}{8}+\frac{1}{6}}}\\~~~~~=\Large{\frac{1}{\frac{2}{24}+\frac{3}{24}+\frac{3}{24}+\frac{4}{24}}}\\~~~~~=\Large{\frac{1}{\frac{12}{24}}}\\~~~~~=\Large{\frac{24}{12}}\\~~~~~=2[Ω]\)
例題4
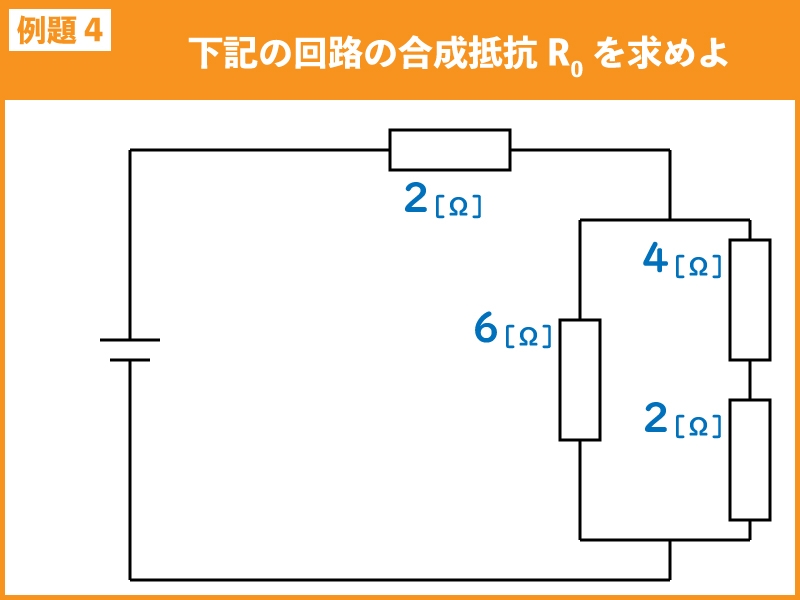
下記の回路の合成抵抗R0を求めよ。
解説
例題4は複雑な回路に見えますが、合成抵抗の公式を活用して1つずつ合成していきましょう。
まず、4Ωと2Ωの直列接続を合成します。
\(R_{42}=4+2\\~~~~~~=6[Ω]\)
次に先ほど合成した6Ωの合成抵抗R42と、その左の6Ωの抵抗の並列接続を合成します。
同じ6Ωの2個の並列接続なので、下記の式で求められます。
\(R_{66}=\Large{\frac{6}{2}}\\~~~~~~=3[Ω]\)
すると上部の2Ωの抵抗と先ほど合成したR66の直列接続となるので、回路全体の合成抵抗R0は下記の式で求められます。
\(R_{0}=2+3\\~~~~~~=5[Ω]\)






















コメント