【令和5年度（午後）】第一種電気工事士《筆記試験》問2

問題

図のような回路において，抵抗□は，すべて2Ωである。a-b間の合成抵抗値［Ω］は。

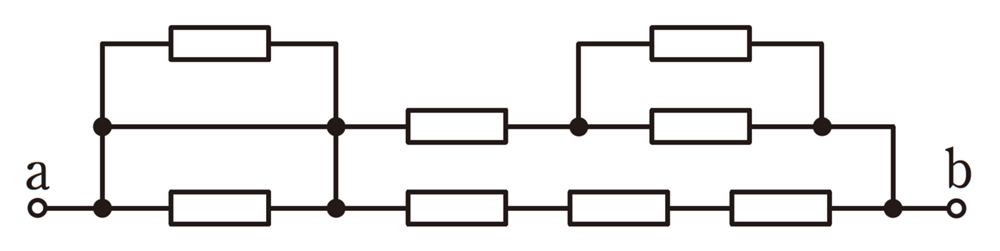
答え

イ．1

ロ．2

ハ．3

ニ．4

『出典：令和5年度第一種電気工事士筆記試験【午後】（問2）』

解説

正解は「ロ．2」です。

この問題のポイントは、合成抵抗の計算についてです。

合成抵抗の公式【電気工事士試験】

電気工事士試験の基本となるのがオームの法則です。オームの法則を駆使して計算問題を解いていきます。 オームの法則の要素の1つに抵抗があります。電気工事士試験では、回路全体の合成抵抗を求めてから、回路全体の電流を求めたりする問題があります。 そ...

denkoubantyou.com

2024.07.25

合成抵抗値の計算の基本を組み合わせて導く問題です。ただし左側の抵抗が無い部分には、注意が必要です。

複雑に見えますが、1つずつ合成していきましょう。

解き方

左側を計算する

左側の抵抗2つが並列に接続されている部分を考えます。

抵抗2つを挟んで真ん中に接続があります。これは抵抗値0Ωなので、上下に抵抗があってもこの部分に電流が流れるので、この部分の合成抵抗値は0Ωとなります。

よって図の左側は0Ωとなります。

右側を計算する

右側部分を計算します。

右上の2つの並列部分は同じ抵抗値なので、合成抵抗値は半分の1Ωとなります。

更に左の抵抗と直列になるので上側は2+1＝3Ωとなります。

下側は3つの直列なので、2+2+2＝6Ωとなります。

上側と下側の並列部分を積／和で求めます。

よって左側0Ωと右側2Ωなので、回路全体の合成抵抗値は2［Ω］となります。