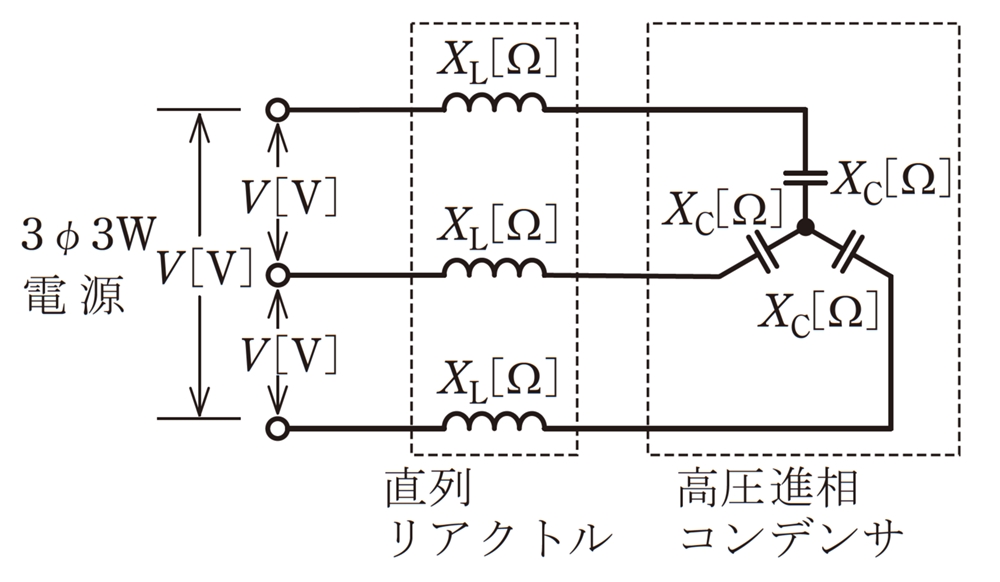
図のように,直列リアクトルを設けた高圧進相コンデンサがある。この回路の無効電力(設備容量)[var]を示す式は。
ただし,XL < XCとする。
答え
イ.\(\Large{\frac{V^{2}}{X_C-X_L}}\)
ロ.\(\Large{\frac{V^{2}}{X_C+X_L}}\)
ハ.\(\Large{\frac{X_CV}{X_C-X_L}}\)
ニ.\(\Large{\frac{V}{X_C-X_L}}\)
『出典:令和5年度第一種電気工事士筆記試験【午後】(問9)』
解説
正解は「イ.\(\Large{\frac{V^{2}}{X_C-X_L}}\)」です。
この問題のポイントは、コンデンサとリアクトルを組み合わせた時の設備容量についてです。
XLとXCの関係を覚えておきましょう。

ボルベア
XLとXCは打ち消しあう!
解き方
相電圧を求める
問題ではY結線となっているので、電源電圧Vを相電圧VYに変換する必要があります。
\(V_Y=\Large{\frac{V}{\sqrt{3}}}・・・①\)
インピーダンスZを求める
XLとXCによるインピーダンスZを求めます。XLとXCは直列に接続されており、XL<XCの関係から次の式となります。
\(Z=X_C-X_L・・・②\)
無効電力Qを求める
無効電力を電圧から導く式は次の通りです。
\(Q=\Large{\frac{V^{2}}{Z}}・・・③\)
上記の式③に前で求めた式①及び式②を代入します。
\(Q=\Large{\frac{V^{2}}{Z}}\\~~~=\Large{\frac{\Large{\frac{V}{\sqrt{3}}}^{2}}{X_C-X_L}}\\~~~=\Large{\frac{\Large{\frac{V^{2}}{3}}}{X_C-X_L}}\\~~~=\Large{\frac{V^{2}}{3(X_C-X_L)}}\normalsize{・・・④}\)
式④は一相の値なので、答えは3倍する必要があります。
よって\(\Large{\frac{V^{2}}{X_C-X_L}}\)が正解となります。






















コメント