電気工事士試験では、電気回路の電圧を求める問題が必ず出題されます。
特に直列接続された2つの抵抗の内、1つの抵抗にかかる電圧を求められる場合があります。
そんな時にオームの法則だけでも解くことは可能ですが、分圧の法則を覚えておくと各段に計算のスピードが上がります。
分圧の法則
下記のような回路において、抵抗R1にかかる電圧VR1はどの様に求めるでしょうか。
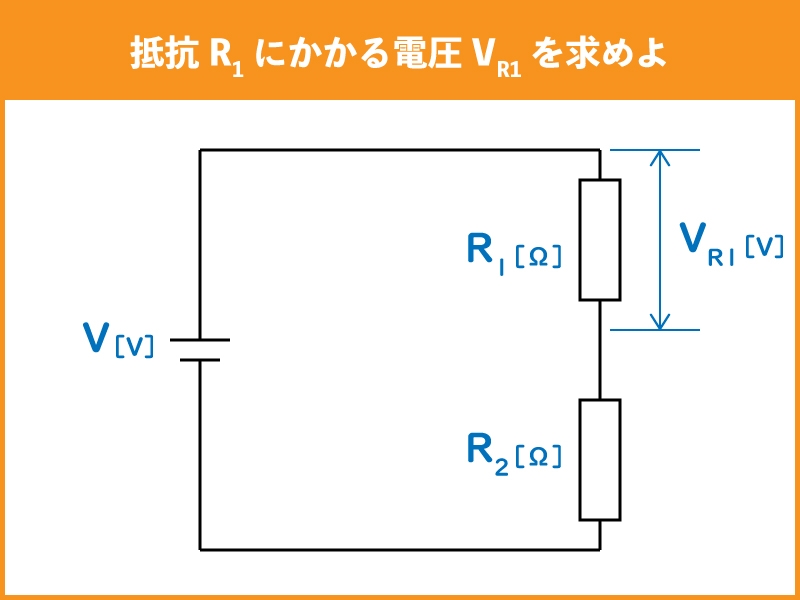
オームの法則を使い、順序を追って地道に導くこともできます。
しかし下記の分圧の法則を使うと一発で導けます。
\(V_{R1}=\Large{\frac{R_1}{R_1+R_2}}\normalsize{V[V]}\)
これを言葉で表すと次のようになります。
\(分圧電圧=\Large{\frac{対象の抵抗}{合成抵抗}}\normalsize{\times電源電圧[V]}\)
また直列に接続される抵抗が3つ以上の場合でも、同様の式で求められます。
例では電源が直流ですが、交流の場合でも同様に求められます。
しかし電源が交流でリアクタンスXが含まれる場合は、合成抵抗は単純な足し算にはなりませんので注意しましょう。合成抵抗はインピーダンスZとなります。
分圧の法則の導出
ここからは分圧の法則が、なぜ成り立つかを導出します。
抵抗R1にかかる電圧VR1は、オームの法則で次の式から求められます。
次に電流Iは、オームの法則で次の式から求められます。
式①に式②を代入します。
これらから分圧の法則が成り立つことが分かります。
練習問題
分圧の法則を解説しました。
ここからは法則を使って、練習問題を解いていきます。
例題1
下記の直流回路において、V1を求めよ。
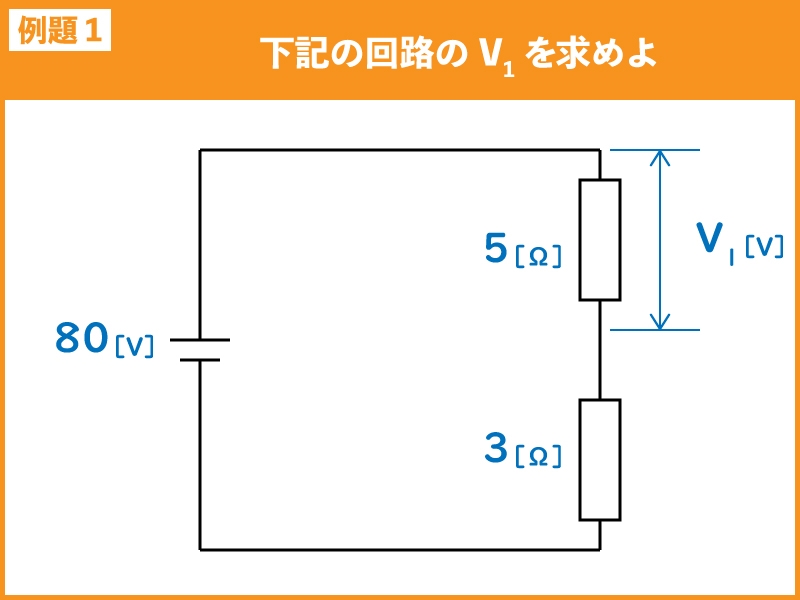
解説
例題1は、下記の式で求められます。
例題2
下記の直流回路において、V2を求めよ。
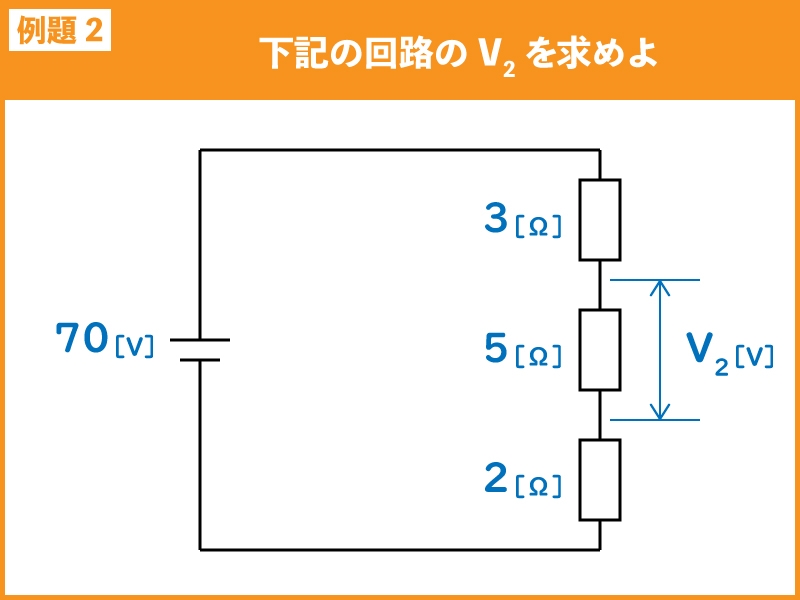
解説
例題2は、下記の式で求められます。
例題3
下記の交流回路において、VCを求めよ。
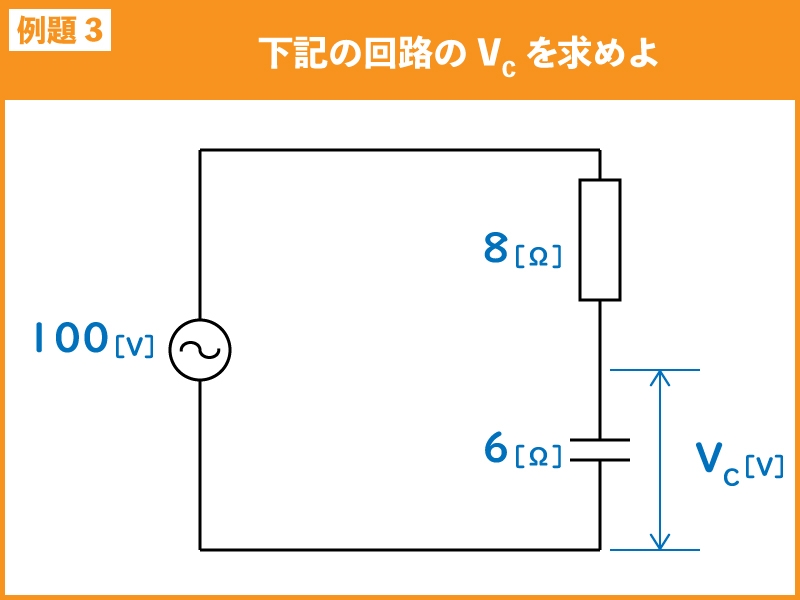
解説
例題3は交流回路でリアクタンスX[Ω]が含まれるので、まずはインピーダンスZを求めます。
求めたインピーダンスZが合成抵抗となります。これから分圧の法則を使って導きます。























コメント