【令和2年度】第一種電気工事士《筆記試験》問4

問題

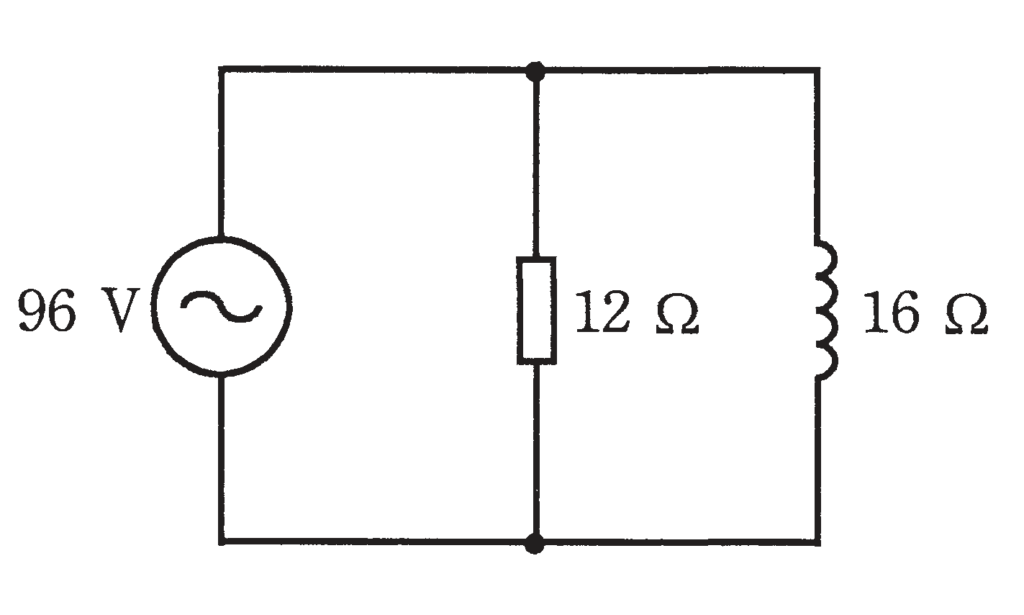
図のような交流回路において，抵抗120Ω,リアクタンス16Ω，電源電圧は96Vである。この回路の皮相電力[V・A]は。

答え

イ．576

ロ．768

ハ．960

ニ．1344

『出典：令和2年度第一種電気工事士筆記試験(問4)』

解説

正解は「ハ．960」です。

この問題では、皮相電力が求められています。この回路で皮相電力を計算するには、回路全体に流れる電流が必要です。電流がわかれば、皮相電力が計算できます。

解き方を2通り紹介します。

解き方①

解き方①は抵抗及びリアクタンスに流れる電流をそれぞれ求め、合成して回路全体の電流を求める方法です。

抵抗及びリアクタンスに流れる電流を求める

抵抗の回路に流れる電流をIR、リアクタンスに流れる電流をILとしてそれぞれ求めます。

\(I_R=\Large{\frac{V}{R}}\\~~~~=\Large{\frac{96}{12}}\\~~~~=8[A]\)

\(I_L=\Large{\frac{V}{X_L}}\\~~~~=\Large{\frac{96}{16}}\\~~~~=6[A]\)

電流を合成する

先ほど求めたIRとILを合成します。交流回路でリアクタンスが含まれるので、単純な足し算では計算できません。

回路全体の電流をI0とすると、次の式で求められます。

\(I_0=\sqrt{{I_R}^2+{I_L}^2}\\~~~~=\sqrt{8^2+6^2}\\~~~~=\sqrt{100}\\~~~~=10[A]\)

皮相電力を求める

皮相電力は電源電圧と回路全体の電流の積で求めら、次の式で計算できます。

\(皮相電力＝VI_0\\~~~~~~~~~~~~=96\times10\\~~~~~~~~~~~~=960[V・A]\)

解き方②

解き方②は抵抗とリアクタンスよりインピーダンスZを計算してから、回路全体の電流を求める方法です。

インピーダンスZを求める

回路全体のインピーダンスZ[Ω]を求めます。抵抗だけの並列回路なら和分の積で求められますが、リアクタンスが含まれるので注意が必要です。

抵抗とリアクタンスの並列回路のインピーダンスZ[Ω]は、次の式で求められます。

\(Z=\Large{\frac{RX_L}{\sqrt{{R}^2+{X_L}^2}}}\\~~~~=\Large{\frac{12\times16}{\sqrt{12^2+16^2}}}\\~~~~=\Large{\frac{192}{\sqrt{400}}}\\~~~~=\Large{\frac{192}{20}}\\~~~~=9.6[Ω]\)

回路全体の電流を求める

先ほど計算した、インピーダンスZから回路全体の電流I0[A]を求めます。オームの法則より、次の式で求められます。

\(I_0=\Large{\frac{V}{Z}}\\~~~~=\Large{\frac{96}{9.6}}\\~~~~=10[A]\)

皮相電力を求める

皮相電力は電源電圧と回路全体の電流の積で求めら、次の式で計算できます。

\(皮相電力＝VI_0\\~~~~~~~~~~~~=96\times10\\~~~~~~~~~~~~=960[V・A]\)