【令和3年度（午前）】第一種電気工事士《筆記試験》問5

問題

図のような三相交流回路において，電流Iの値［A］は。

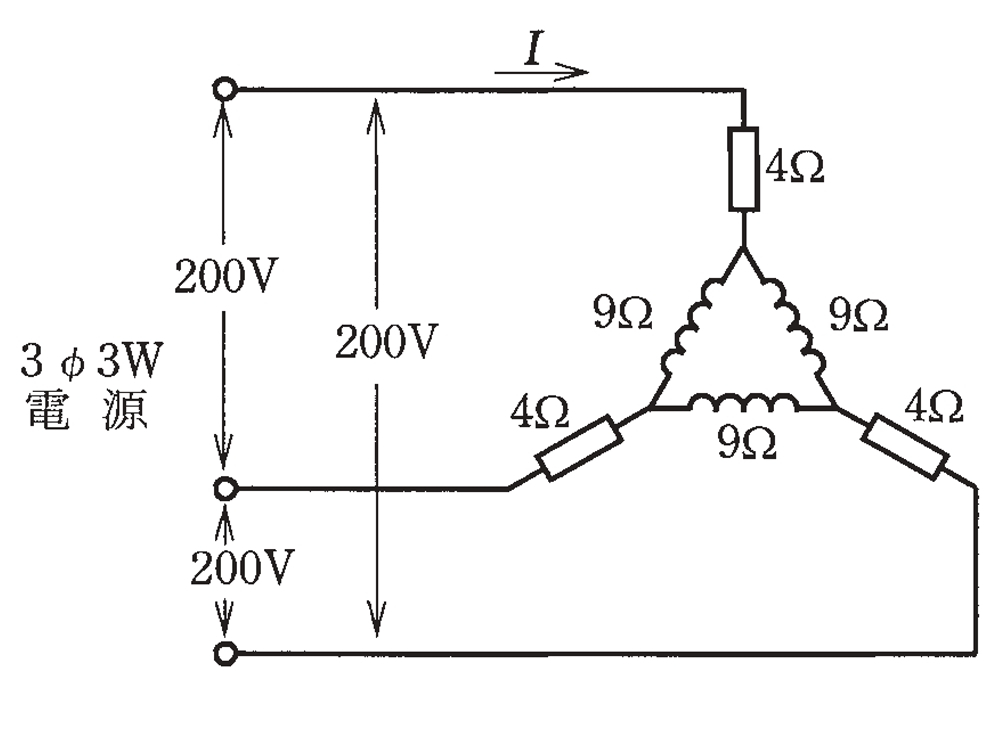
答え

イ．\(\Large{\frac{200\sqrt{3}}{17}}\)

ロ．\(\Large{\frac{40}{\sqrt{3}}}\)

ハ．\(40\)

ニ．\(40\sqrt{3}\)

『出典：令和3年度第一種電気工事士筆記試験【午前】（問5）』

解説

正解は「ロ．\(\Large{\frac{40}{\sqrt{3}}}\)」です。

この問題のポイントは誘導性リアクタンス（X_L）のΔ-Y変換です。誘導性リアクタンス（X_L）のΔ結線部分をY結線に変換できれば、1個の単純なY結線の回路となります。

誘導性リアクタンス（X_L）をΔ回路からY回路に変換するには、値を1/3にすればいいです。これを知っていれば簡単に解ける問題です。

ボルベア

誘導性リアクタンス（X_L）をΔからYに変換しよう！

解き方

回路をY結線に変換する

Δ結線されている誘導性リアクタンス（X_L）部分をY結線にします。

値が同じなので、Δ結線時の値の1/3にするとY結線に変換できます。変換前をX_LΔ、変換後をX_LYとすると次の通りです。

よって4Ωの抵抗と3Ωの誘導性リアクタンスの直列回路のY結線となります。

インピーダンス（Z）を求める

電流を求めるには、インピーダンス（Z）が必要です。

抵抗（R）と誘導性リアクタンス（X_LY）から、次の式でZを求めます。

インピーダンスの求め方について詳しくは、こちらをご覧ください。

インピーダンス（Z）を求める公式

電気工事士試験では、頻繁にインピーダンス（Z）を求める問題が出題されます。 インピーダンスを求める問題もあれば、他のものを求める途中で計算が必要な場合もあります。 インピーダンスは必ず覚えておきたい必須項目です。 インピーダンスの基礎 イン...

denkoubantyou.com

2023.03.24

電流（I）を求める

問題で求められているのは、電流（I）は線電流です。

今回はY結線なので線電流は、相電圧とインピーダンス（Z）から求められます。問題に記されている電圧は線間電圧なので、相電圧に変換する必要があります。

相電圧は線間電圧の\(\Large{\frac{1}{\sqrt{3}}}\)となります。

これらから次の式で電流（I）が求められます。相電圧をE、線間電圧をVとします。