問題
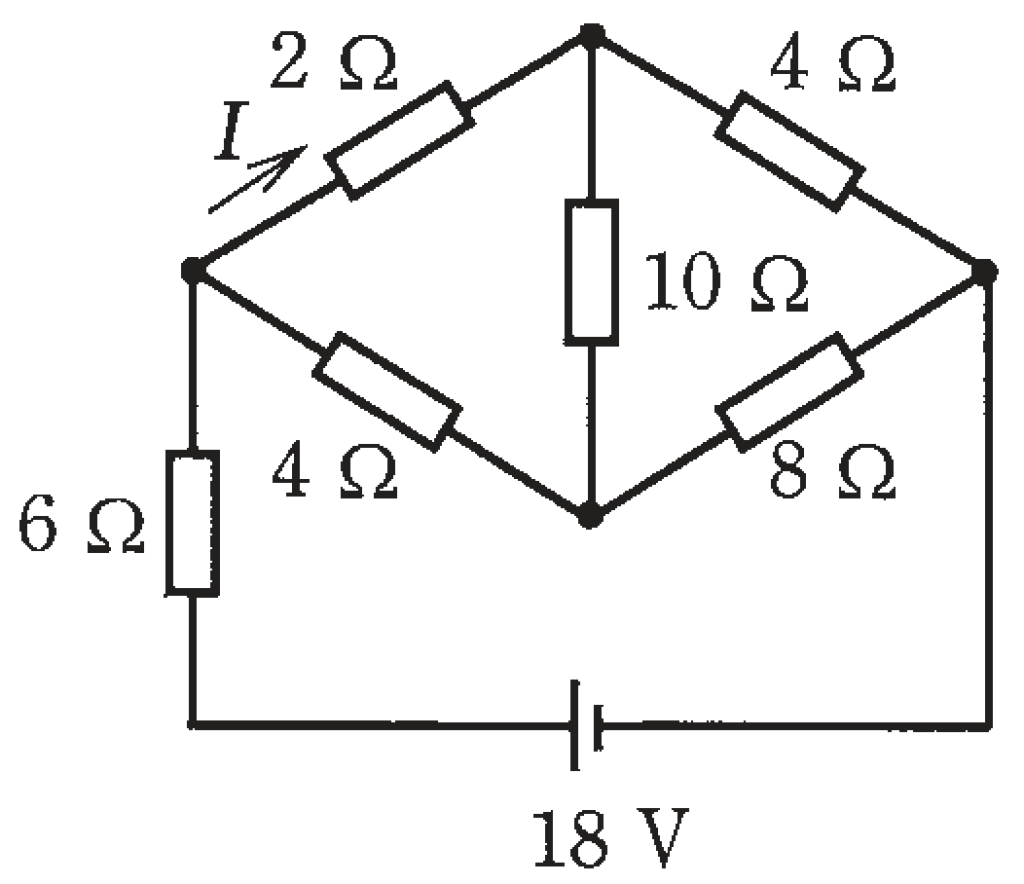
図のような直流回路において,抵抗2Ωに流れる電流I[A]は。
ただし,電池の内部抵抗は無視する。
答え
イ.0.6
ロ.1.2
ハ.1.8
ニ.3.0
『出典:平成28年度第一種電気工事士筆記試験(問2)』
解説
正解は「ロ.1.2」です。
この問題のポイントは、ブリッジ回路の平衡による抵抗の無視です。
この回路はブリッジ回路があります。ブリッジ回路が平衡していると、中央の抵抗10Ωを無視することができます。
平衡の条件は、ひし形の対面の抵抗2つの積が等しい時です。
この回路では、2Ω×8Ωと4Ω×4Ωはどちらも16なので平衡しています。よって10Ωの抵抗は無視できます。
後は通常の計算で電流Iを求めます。

ボルベア
ブリッジ回路は平衡していると中央の抵抗は無視できる!
解き方
ブリッジ回路部の抵抗を合成する
まずブリッジ回路部分の抵抗を合成します。
10Ωの抵抗は無視できるので、直並列回路になります。
和分の積により抵抗を合成します。この抵抗をR1とします。
\(R_1=\Large{\frac{(2+4)\times(4+8)}{(2+4)+(4+8)}}\\~~~~~=4[Ω]\)
R1にかかる電圧V1を求める
この問題ではブリッジ回路だけでなく、直列に6Ωの抵抗が接続されています。
よって先ほど求めた合成抵抗R1(ブリッジ回路部)にかかる電圧を分圧の式にて求めます。この電圧をV1とします。
\(V_1=\Large{\frac{4}{6+4}}\normalsize{\times18}\\~~~~=\Large{\frac{72}{10}}\\~~~~=7.2[V]\)
電流Iを求める
先ほどの計算で、ブリッジ回路部にかかる電圧V1が求められました。
これから電流Iを求めます。
\(I=\Large{\frac{V_1}{2+4}}\\~~=\Large{\frac{7.2}{6}}\\~~=1.2[A]\)
よって答えは1.2[A]となります。























コメント